Reference no: EM132263180

Questions -

Question 1 - The following partial differential equation (PDE) describes the temperature u(x, t) in a metal rod of length 1, where the temperature at the right hand end is equal to 1, and the temperature at the left hand end starts at zero and tends towards 1 as time increases:

∂u/∂t = D ∂²u/∂x², u(0, t) = 1- e^-at, u(1, t) = 1, u(x, 0) = x.

In this equation, D and a are positive constants.

(a) Let u(x, t) = 1 - e^-at (1 - x) + u^∼(x, t) and write down the PDE, as well as initial and boundary conditions, for u^∼(x, t). Explain briefly (one sentence) why this is a useful substitution to make.

(b) Assume u^∼(x, t) has the eigenfunction expansion

u^∼(x, t) = _n=1∑^∞A_n(t)sin(nπx).

Explain briefly (one sentence) why the eigenfunctions sin(nπx) are appropriate for this problem. Find the solution to u^∼(x, t), and therefore u(x, t), by solving for the coefficients A_n(t), assuming that a ≠ Dn²π² for any n ∈ (1, 2, 3, . . .).

You may use the following Fourier sine series expansion:

1 - x = _n=1∑^∞(2/nπ)sin(nπx).

(c) Determine how the solution is changed if a = Dk²π² for some k ∈ {1, 2 ,3, . . .}.

(d) Use Python or similar to create a plot of u(x, t) with a = 10, D = 1, for a few values of t between 0 and 1.

Question 2 - The steady temperature on an infinite domain satisfies the following partial differential equation:

∂²u/∂x² + ∂²u/∂y² = 0, -∞ < x < ∞, 0 < y < 1,

with boundary conditions

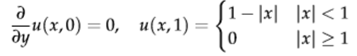
(a) Using the integral definition, compute the Fourier transform of the boundary condition u^{^}(k, 1) = F[u(x, 1)].

(b) Use the Fourier transform method to find an expression for the solution u. You should obtain the solution in terms of a real-valued integral.

(c) Use Python or similar to numerically evaluate the integral solution to u found in part (b), creating a plot of u on y = 0, for -3 < x < 3. You should take the upper limit of the integral up to k = 20. Note that in order to compute the integral, you may have to work out the value of the integrand at k = 0 by hand.