Reference no: EM131081393

Math 104: Final exam-

1. Suppose that (s_n) is an increasing sequence with a convergent subsequence. Prove that (s_n) is a convergent sequence.

2. (a) Let f_n be functions defined on R as

f_n(x) = x/n²(1 + nx²),

for all n ∈ N. By using the Weierstrass M-test, or otherwise, prove that ∑ f_n converges uniformly on R.

(b) Consider the sequence of functions defined on R as

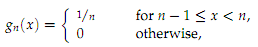
for all n ∈ N. Define M_n = sup{|g_n(x)| : x ∈ R}. Prove that ∑g_n converges uniformly to a limit g, but that ∑M_n diverges. Sketch g(x) for 0 ≤ x < 5.

3. Consider the sequence (sn) defined according to s₁ = 1/3 and s_n+1 = λs_n(1 - s_n) for n ∈ N, where λ is a real constant.

(a) Prove that (s_n) converges for λ = 1.

(b) Prove that (s_n) has a convergent subsequence for λ = 4.

(c) Prove that (s_n) diverges for λ = 12.

4. A real-valued function f on a set S is defined to be Lipschitz continuous if there exists a K > 0 such that for all x, y ∈ S,

| f(x) - f(y)| ≤ K|x - y|.

(a) Prove that if f is Lipschitz continuous on S, then it is uniformly continuous on S.

(b) Consider the function f(x) = √x on the interval [0, ∞). Prove that it is uniformly continuous, but not Lipschitz continuous.

5. Consider the function defined on the closed interval [a, b] as

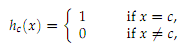
where a < c < b.

(a) Prove that h_c is integrable on [a, b] and that _a∫^b hc = 0.

(b) Suppose f is integrable on [a, b], and that g is a function on [a, b] such that f(x) = g(x) except at finitely many x in (a, b). Prove that g(x) is integrable and that _a∫^b f = _a∫^b g. You can make use of basic properties of integrable functions.

6. Consider the sequence of functions hn on R defined as

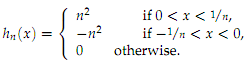
(a) Sketch h₁ and h₂.

(b) Prove that h_n converges pointwise to 0 on R.

(c) Let f be a real-valued function on R that is differentiable at x = 0. Prove that

lim_{n→∞ -∞}∫^∞h_n f = f'(0).

7. (a) Find an example of a set A ⊆ R where the interior A^o is non-empty, but that sup A ≠ sup A^o and inf A ≠ inf A^o.

(b) Let B₁, . . . , B_n be subsets of R. Prove that

(_i=1∩ⁿ B_i)^o = _i=1∩ⁿ B^o_i.

(c) Suppose that {C_i}^∞_i=1 is an infinite sequence of subsets of R. Prove that

(_i=1∩^∞ C_i)^o ⊆ _i=1∩^∞ C^o_i.

but that these two sets may not be equal.

8. (a) If f is a continuous strictly increasing function on R, prove that d(x, y) = |f(x) - f(y)|

defines a metric on R.

(b) Prove that d is equivalent to the Euclidean metric dE(x, y) = |x - y|.

(c) Suppose g is a continuous strictly increasing function on [0, ∞) where g(0) = 0. Is the function

d₂(x, y) = g(|x - y|)

always a metric? Either prove the result, or find a counterexample.

9. Consider the continuous function defined on R as

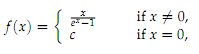
where c ∈ R. For this question you can assume basic properties of the exponential, such that it is continuous, differentiable, and has the Taylor series e^x = _k=0∑^∞ x^k/k!.

(a) Use L'Hopital's rule to compute lim_x→0 f(x) and hence determine c.

(b) Show that f is differentiable on R and compute f'.

(c) Use the above results to write down the partial Taylor series

f_T(x) = _k=0∑¹f^(k)(0)x^k/k!.

Calculate the function limits lim_x→∞ f(x) and lim_x→-∞(x + f(x)) and use the results to sketch f and f_T on (-10, 10).

10. Given a function f on [a, b], define the total variation of f to be

Vf = sup{_k=1∑ⁿ|f(t_k)-f(t_k-1)|}

where the supremum is taken over all partitions P = {a = t₀ < t₁ < . . . < t_n = b} of [a, b].

(a) Calculate Vf for the function defined on [-1, 1] as

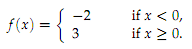
(b) Prove that if f is differentiable on an interval [a, b] and that f' is continuous then Vf = _a∫^b|f'|.