Reference no: EM132230560

Tensor Algebra and Tensor Analysis -

Assignment 1 -

Q1. A coordinate system r(θ¹, θ²) in E² is defined by

r = 2exp(θ¹) θ²e₁ + (θ¹-2θ²)²e₂,

where the vectors e_i (i = 1, 2) form an orthonormal basis. For the point θ¹ = 0, θ² = 1/2

a) Calculate the vectors g_i (i = 1, 2) tangent to the coordinate lines.

b) Calculate the basis gⁱ (i = 1, 2) dual to g_i (i = 1, 2).

c) Calculate the Christoffel symbols of the first and second kind Γ_ijk and Γⁱ_jk, respectively.

Q2. Let A = A_i^j gⁱ ⊗ g_j and B = Bⁱ_j g_i ⊗ g^j, where

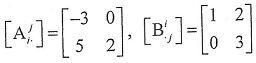
and vectors g_i, gⁱ (i = 1, 2) are the same as in Problem 1.

a) Compute the components C^ij, C_ij, Cⁱ_j and C_jⁱ of the tensor C = AB^T.

b) Evaluate exp(A).

Q3. Express div t(r) and grad div t(r) of the vector function t(r) defined by t(r) = 1/||r|| (r+b), where r, b ∈ E³ and b is a constant vector.

Assignment 2 -

Q1. A coordinate system r(θ¹, θ²) in E² is defined by

r = θ(cosθ²e₁ + ½sinθ²e₂),

where the vectors e_i (i = 1, 2) form an orthonormal basis. For the point θ¹ = 2, θ² = π/4

a) Calculate the vectors g_i (i = 1, 2) tangent to the coordinate lines.

b) Calculate the basis gⁱ (i = 1, 2) dual to g_i (i = 1, 2).

c) Calculate the Christoffel symbols of the first and second kind Γ_ijk and Γⁱ_jk, respectively.

Q2. Let A = A_i^j gⁱ ⊗ g_j and B = Bⁱ_j g_i ⊗ g^j, where

and vectors g_i, g^j(i = 1, 2) are the same as in Problem 1.

a) Evaluate the tensor (B²)^T.

b) Compute the components C^ij, C_ij, Cⁱ_j and C_jⁱ of the tensor C = A(B²)^T.

c) Check whether the tensors A and (B²)^T are commutative or not.

d) Compute B² : A.

Q3. Let a = e₁ -2e₂ be a vector in E³, where e_i (i = 1, 2, 3) form an orthonormal basis. Calculate a vector obtained from a by rotation by the angle ω = π/3 about an axis along the vector d = -e₂ + e₃.

Note - Need solution of questions 2 of both assignemtns.