Reference no: EM132377271

AP Calculus AB review Assignment -

Part A -

SOLVE THE FOLLOWING -

Q1. 3w - 4 = 5

Q2. x³ - 7x² + 12x = 0

SHOW YOUR WORK.

Q3. Find the equation of the line going through (-3, 4) and (3, 10).

Q4. Find the equation of a line going through (2, 1) with a slope 3/2.

Q5. Find the equation of the line perpendicular to y = (2/3)x - 5 and passes through (2, 1).

Q6. Divide (2x³ - 4x² + 3x) by (x - 3).

Q7. Find [f(g(x))] for f(x) = 4x - 1 and g(x) = 2x + 5.

Q8. Solve the system of equations

3x + 5y = 7

3x + 2y= 1

Q9. Solve x - √(x+2) = 6.

Q10. Solve |3 -2x| ≥ 5.

Q11. State the domain and range of {(2, 1), (3, 4), (4, 8)). Explain why or why it is not a function.

Q12. Solve 2 = (y + 3)(2y - 2).

Q13. Find the domain f(x) = (5x - 1)/(x² + 8x + 15).

Q14. Use the quadratic equation formula to solve x² + 3x - 5 = 0.

Q15. Find the critical point of y = 3(x - 2)² + 3. Is it a max or min?

Q16. Find the critical point of y = -2(x + 1)² - 4. Is it a max or min?

Q17. Explain in your own words when you would use the Law of Sines to solve for the missing parts of a triangle. When would you need to use the Law of Cosines?

Q18. Solve 5 = e^0.4t for t.

Q19. Find the inverse of f(x) = 2x + 7.

Q20. Graph the following functions on one set of axes. Describe the changes with regard to vertices and position on axes

y = x²

y = x² + 2

y = (x - 3)²

y = (x - 3)² + 2

Use the information from the previous problem to discuss the chances below:

Compare	# units shift left	# units shift right	# units shift up	# units shift down
Q21. y = x3 to y = -2x3
Q22. y = x3 to y = (x-5)3
Q23. y = x3 to y = x3 + 12
Q24. y = |x| to y = |x+15|-9

Fill in the table for the given trig equations.

	Amplitude	Period	Phase shift
Q25. y = -3 sinx
Q26. y = cos4x
Q27. y = cos x + 2
Q28. y = -4 sin2x
Q29. y = 10sin(x/4 - 4π) - 5

Q30. Graph y = 2 cos ½x.

Q31. How can you tell whether f(x) defines a function by looking at its graph?

Q32. A parabola y = ax² + bx + c has vertex (4, 2). If (2, 0) is on the parabola, then find the value of abc.

Q33. A rectangular field is twice as long as it is wide. Express the area of the rectangle as function of its perimeter P.

Q34. A vendor sells large sodas for $.70 and small sodas for $.50. One afternoon, he sold 1000 sodas for a total of $580. How many large sodas did he sell?

Q35. Find the future value to the nearest dollar of $5000 invested at 8% for 5 years in an account that compounds interest continuously.

Q36. The distance from city A to city B is 150 miles. From city A to city C is 90 miles. Which of the following is necessarily true?

a. The distance from B to C is 60 miles.

b. Six times the distance from A to B equals 10 times the distance from A to C.

c. The distance from B to C is 240 miles.

d. The distance from A to B exceeds by 30 miles twice the distance from A to C.

e. Three times the distance from A to C exceeds by 30 miles twice the distance from A to B.

Be sure to explain your thinking.

Q37. Solve the triangle

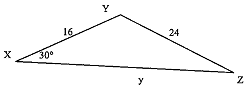
Q38. Solve 2sin²x + sin x - 1 = 0.

Q39. If sin A = 2/5 and A is in Quadrant II, find cos A.

Q40. If tan B = 12/5 and B is in Quadrant I, find sin 2B.

Q41. Change 7π/6 radians to degree measure.

Q42. Change 200^o to radian measure.

Q43. Find the reference angle for - 120^o.

Q44. Solve √(x-5) = ³√(x-3).

Use reflections, rotations, transformations of y = x² to sketch the graphs in #'s 45 - 48.

Q45. y = 1 + (x - 2)²

Q46. y = 2 - (x+1)²

Q47. y = -2(x + 1)² - 3

Q48. y = x² + 6x

Given f(x) = 2x and g(x) = x²+1, find formulas and domains for #'s 49-53.

Q49. f + g

Q50. f - g

Q51. fg

Q52. f/g

Q53. f(g(x))

Q54. f(x) = √(x+5) and g(x) = 2x + 8, find f(g(-3)).

Q55. A locomotive travels on a straight track at a constant speed of 40mph, then reverses direction and returns to its starting point, traveling at a constant speed of 60mph.

a. What is the average velocity for the round trip?

b. What is the average speed for the round trip?

c. What is the total distance traveled by the train if the trip took 5 hours?

Q56. Given that f(x) = 2x + 1, find a function g(x) such that f(g(x)) = x.

Use the equation y = 1 + √x to answer the #'s 57 - 60.

Q57. For what values of x is y = 4?

Q58. For what values of x is y = 0?

Q59. For what values of x is y ≥ 6?

Q60. Does y have a minimum value? A maximum value? If so, define them.

Q61. If you had a device that could record the temperature of a room continuously over a 24 - hour period, would you expect the graph of temperature versus time to be a continuous (unbroken) curve? Explain.

Q62. If you had a computer that could track the number of boxes of cereal on the shelf of a market continuously over a one week period, would you expect the graph of the number of boxes on the shelf versus time to be continuous (unbroken) curve? Explain your reasoning.

Q63. The diagram below shows a field ABCD with a fence BD crossing it. AB = 15m, AD = 20m, and angle BAD = 110^o • BC = 22m and angle BDC = 30^o.

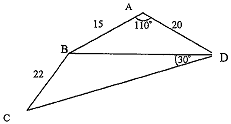
(a) Calculate the length of BD.

(b) Calculate the size of angle BCD.

(c) Write down the length of BD correct to 1 significant figure.

(d) Find the size of angle BCD that the student calculated, giving your answer correct to the 1 decimal place.

Q64. Determine the asymptotes and/or holes for the following graph

f(x) = (2x² - 5x - 3)/(x² + 2x - 1)

Q65. In economics, the demand function relates the price per unit of an item to the In economics the demand function relates the price per unit of an item to the number of units that consumers will buy at that price. The demand, q, is considered to be the independent variable, while the price, p, is considered to be the dependent variable.

Suppose that in a certain market, the demand function for widgets is a linear function

p = -0.75q + 54,

where p is the price in dollars and q is the number of units (hundreds of widgets in this case).

a. What is the slope of this function? Explain the meaning of the sign of the slope in practical terms.

b. Find the p- and q- intercepts for this function. What is the significance of these intercepts in the context of the problem?

Q66. Celia has $20000 to invest. There are two different options that she can choose.

Option 1: The investment grows at a rate of 3.5 % compound interest each year.

Option 2: The total value of the investment increases by $800 each year.

The money is to be invested for 15 years.

(a) Copy and complete the table below giving the values of the investments to the nearest dollar for the first 4 years.

Year	0	1	2	3	4
Option 1	20000	20700
Option 2	20000	20800

(b) Calculate the values of each investment at the end of 15 years.

(c) If Option 1 is chosen find the total number of complete years before the values of the investment is first greater than $25000.

(d) If Option 2 is chosen calculate the percentage increase in the investment for the final year.

Part B -

Q1. What is the end behavior of the function 3x⁷ + 2x⁶ - 3x⁴ - x² + x - 46?

(A) As x→ -∞, f→ - ∞ , and as x→∞ , f→ -∞.

(B) As x→ -∞, f→ ∞, and as x→∞, f→ -∞.

(C) As x→ -∞, f→ ∞, and as x→ ∞, f→ ∞.

(D) As x→ -∞, f→ -∞, and as x→ ∞, f→ infty.

Q2. What is (x⁴+13x³+25x²-105x+52)/(x²+5x-4)?

(A) x³ - x² + 5x - 13

(B) x² + 13x - 7

(C) x² + 7x - 13

(D) x² - 3x + 13

Q3. Which of the following polynomials have exactly three real roots, x = 1, -1, and 3?

(A) x⁴ -3x² + 2x - 8

(B) x⁴ - x³ - 7x² + x + 6

(C) x⁵ -3x⁴ - x + 3

(D) x⁴ + 3x² - 4

Q4. What is the remainder of (x³-3x²+4x+5)/(x-4)?

(A) 18

(B) 38

(C) 0

(D) 28

Q5. How many possible positive and negative real roots does the function x³ - 4x² + 3x - 2 have?

(A) 1 or 3 positive, 0 negative

(B) 0 or2 positive, and 1 negative

(C) 0 positive and 1 negative

(D) 1 positive and 0 or 2 negative

Q6. The function (x²-4x+3)/(x-2) has what asymptotes, if any?

(A) A vertical asymptote at x = 2

(B) A horizontal asymptote at x = 3

(C) A vertical asymptote at x = 0 and an oblique asymptote at y = x

(D) A vertical asymptote at x = 2 and an oblique asymptote at y = x - 2

Q7. Which of the following expressions is not equal to the others?

(A) log_ax

(B) ln x/ln a

(C) log a/log x

(D) 1/log_xa

Q8. The exponential rate of decay of a substance is .08 per year. What is the half-life of this substance in years?

(A) 12.5 years

(B) ≈56.5 years

(C) ≈8.66 years

(D) ≈10.035 years

Q9. Which of the following bank accounts will be worth the most in 10 years?

(A) $11,000 at 10% simple interest

(B) $9,450 at 9.0% compounded daily

(C) $9,800 at 8.5% compounded continuously

(D) $9,500 at 9.0% compounded quarterly

Q10. In which quadrants do sine and cosine have the same sign?

(A) I and II

(B) I and IV

(C) II and III

(D) I and III

Q11. Which of the following is a formula for all of the quadrantal angles?

(A) 0 ≤ θ < 2π

(B) θ = nπ/2, where n is an integer

(C) θ = 2nπ, where n is an integer

(D) θ = ((3n/2) +1)^π/2, where n is an integer

Q12. Which of the following is not equal to the others?

(A) sin(π/2)

(B) cos(2π)

(C) tan 5π/4

(D) csc 3π/2

Q13. Which expression is unequal to the others?

(A) sin²(x)csc²(x)

(B) cos²(x) - sin²(x)

(C) sec²(x) - tan²(x)

(D) csc²(x) - cot²(x)

Q14. Which of the following does not solve the equation sin(x)cos(x) = 0?

(A) x = 2π/4

(B) x = 3π/3

(C) x = 12π/4

(D) x = 5π/4

Q15. What is the amplitude and period of the function f(x) = 2 cos(2x)?

(A) Amplitude: 1; Period: 2π

(B) Amplitude: 1/2; Period: π

(C) Amplitude: 4; Period: 1/2

(D) Amplitude: 2; Period: π

Q16. Which value is defined?

(A) arcsin(2)

(B) arctan(0)

(C) tan(π/2)

(D) sec(π/2)

Part C - Trigonometric Identities

I. Pythagorean Identities

A. sin²θ + cos2θ = 1

B. tan²θ + 1 = sec²θ

C. cot²θ + 1 = csc²θ

II. Sum and Difference of Angles Identities

A. sin(α + β) = sinα cosβ + cosα sinβ

B. sin(α - β) = sinα cosβ - cosα sinβ

C. cos(α + β) = cosα cosβ - sinα sinβ

D. cos(α - β) = cosα cosβ + sinα sinβ

E. tan(α + β) = (tanα + tanβ)/(1 - tanα tanβ)

F. tan(α - β) = (tanα - tanβ)/(1 + tanα tanβ)

III. Double Angle Identities

A. sin(2θ) = 2sinθ cosθ

B. cos(2θ) = cos²θ - sin²θ

= 2cos² - 1

= 1 - 2 sin²θ

C. tan(2θ) = 2tanθ/(1-tan²θ)

IV. Half Angle Identities

A. sin θ/2 = ±√((1-cosθ)/2)

B. cos θ/2 = ±√((1+cosθ)/2)

C. tan θ/2 = ±√((1-cosθ)/(1+cosθ))

Inverse Trig Functions -

A. y = sin^-1x if and only if x = sin y where -π/2 ≤ y ≤ π/2.

B. y = cos^-1x if and only if x = cos y where 0 ≤ y ≤ π.

C. y = tan^-1x if and only if x = tan y where  -π/2 ≤ y ≤ π/2.

Find the exact value of each expression:

1. cos^-1 0

2. sin^-1(-½)

3. tan^-1√3

4. cos^-1(√3/2)

5. tan^-11

6. sin^-11

Use a calculator to find each value.

7. sin^-1(- 3/7)

8. tan^-1(5.1)

9. cos^-1√3/5

Find the exact value of each expression.

10. sin[sin^-1(0.24)]

11. tan^-1(tan 3π/7)

12. cos^-1(cos π/3)

Inverse Trig Functions Continued -

I. Inverse Trig Functions

A. y = csc^-1x if and only if csc y = x and -π/2 ≤ y ≤ π/2.

B. y = sec^-1x if and only if sec y = x and 0 ≤ y ≤ π.

C. y = cot^-1x if and only if cot y = x and 0 ≤ y ≤ π.

Find the exact value of each expression.

1. cos(sin^-1 √3/2)

2. tan[sin^-1(- √2/2)]

3. sec[cos^-1(½)]

4. csc(cos^-10)

5. sin(tan^-14)

6. cot^-1(cot 2π/3)

7. cos^-1(cos 4π/3)

Find the exact value of each.

8. sec^-1 2√3/3

9. cot^-1(-1)

10. csc^-12

Use a calculator to find each value.

11. cot^-1(6.1)

12. sec^-1(-4)

Trigonometric Identities

I. Reciprocal Identities

A) sinθ = 1/cscθ

B) cosθ = 1/secθ

C) tanθ = 1/cotθ

D) cscθ = 1/sinθ

E) secθ = 1/cosθ

F) cotθ = 1/tanθ

II. Quotient Identities

A) tanθ = sinθ/cosθ

B) cotθ = cosθ/sinθ

III. Pythagorean Identities

A) sin²θ + cos²θ = 1

B) tan²θ + 1 = sec²θ

C) cot²θ + 1 = csc²θ

Simplify each expression.

1. csc²θ - 1

2. (1 - sinx)(1 + sinx)

3. sin²θ(csc²θ - 1)

4. cosθ tanθ cscθ

5. cscθ/(1 + cot²θ)

6. 1/sin²θ - 1/tan²θ

7. sin²x + sin²xcot²x

Trig Identities

I. Guidelines for Verifying Trig Identities

A. Begin with the most complicated side

B. Work on one side only

C. Rewrite sums or differences of quotients as one single quotient

D. Rewrite in terms of sine and cosine only

E. Factor (GCF or Difference of Squares)

F. Multiply (Foil or Distributive Property)

Verify each identity.

1. cscθ sinθ - sin²θ = cos²θ

2. sinθ(cotθ + tanθ) = secθ

3. (cscθ + cotθ)(cscθ - cotθ) = 1

4. csc⁴θ - csc²θ = cot⁴θ + cot²θ

5. cscx + cot x = sinx/(1-cosx)

6. 8csc²θ - 3cot²θ = 3 + 5csc²θ

7.  1/(1 - secθ) + 1/(1 + secθ) = -2cot²θ

Sum and Difference Formulas

I. Sum and Difference Identities

A. cos(α + β) =

B. cos(α - β) =

C. sin(α + β) =

D. sin(α - β) =

E. tan(α + β) =

F. tan(α - β) =

Find the exact value of each expression.

1. cos π/12

2. tan105^o

3. sin 13π/12

4. csc(-15^o)

5. sin40^o cos20^o + cos40^o sin20^o

6. cos100^o cos80^o - sin100^o sin80^o

Find each of the following.

a) sin(α + β)

b) tan (α - β)

7. sin α = ½, 0 < α < π/2

cos β = √7/3, -π/2 < β < 0

8. Verify:

cos(π+θ) = -cosθ

Double-Angle and Half-Angle Identities -

I. Double Angle Identities

A) sin2θ = 2sinθcosθ

B) cos2θ = cos²θ - sin²θ

= 2cos²θ - 1

= 1 - 2sin²θ

C) tan2θ = 2tanθ/(1-tan²θ)

II. Half Angle Identities

A) sinθ/2 = ±√((1-cosθ)/2)

B) cosθ/2 = ±√((1+cosθ)/2)

C. tanθ/2 = ±√((1-cosθ)/(1+cosθ))

where + or - is determined by θ/2.

Find the exact value of each expression.

a) sin(2θ)

b) cos(2θ)

c) sin(θ/2)

1. sinθ = 12/13, 0 < θ < θ/2

2. tanθ = 15/8,  π < θ < 3π/2

Use the half angle identity to find each exact value.

3. sin 5π/8

4. tan22.5^o

Find the exact value.

5. sin(2cos^-1 √3/2)

6. cos(sin^-1 5/13)

Trig Equations (I)

Solve each equation for 0 ≤ θ < 2π.

1. sinθ = √3/2

2. cotθ = √3/3

3. cosθ = -1/2

4. sin(2θ) = - √2/2

5. 2 tan θ - 1 = 1

6. 4 sin² θ - 3 = 0

7. csc 3θ/2 = -2√3/3

8. cot(θ/2 - π/6) = 1

Trig Equations (II)

I. Solving Trig Equations

A) Set trig function equal to a numerical value

B) Apply trig identities to rename expression in terms of one trig function

C) Factor:

1. GCF

2. Product of binomials

D) Divide cosθ to produce tanθ

Solve for 0 ≤ θ < π.

1. cos² θ - cos θ = 0

2. 2sin² θ - 3 sin θ + 1 = 0

3. (cot θ - 1)(csc θ + 1) = 0

4. 2cos² θ = sin θ +1

5. √3 sin θ = cos θ

6. sin 2θ + sin θ = 0

7. cos 2θ = 1- sin θ

8. sin θ tan θ = √3 sin θ.