This notation bounds a function to in constant factors. We say f(n) = Θ(g(n)) if there presents positive constants n₀, c₁ and c₂ such that to the right of n₀ the value of f(n) always lies between c1g(n) and c2g(n), both inclusive. The given Figure gives an idea about function f(n) and g(n) where f(n) = Θ(g(n)) . We will say that the function g(n) is asymptotically tight bound for f(n).

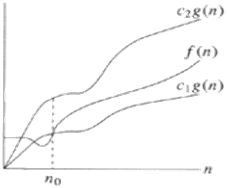
Figure: Plot of  f(n) = Θ(g(n))

For instance, let us show that the function f(n) =  (1/3) n²   - 4n = Θ(n²).

Now, we must determined three positive constants, c ₁, c ₂ and n_o as

c₁n² ≤1/3 n² - 4n ≤ c₂ n² for all n ≥ no

⇒ c₁ ≤ 1/3- 4/n  ≤ c₂

By choosing no = 1 and c₂ ≥ 1/3 the right hand inequality holds true.

Likewise, by choosing n_o = 13, c₁  ≤  1/39, the right hand inequality holds true. Thus, for c1 = 1/39 , c₂ = 1/3 and n_o  ≥ 13, it follows that 1/3 n² - 4n = Θ (n²).

Surely, there are other alternative for c₁, c₂ and no. Now we might illustrates that the function f(n) = 6n³    ≠  Θ (n₂).

In order to prove this, let us suppose that c₃ and no exist such that 6n³   ≤ c₃n²  for n ≥ n_o, But this fails for adequately large n. Therefore 6n³    ≠  Θ (n²).