Properties of Bezier Curves - modeling and rendering

A very helpful property of a Bezier curve is that it always passes via the first and last control points. Such the boundary conditions at the two ends of the curve are as:

P(0) = p 0

P(1) = p n

Values of the parametric first derivatives of a Bezier curve on the end points can be computed from control-point coordinates as

P' (0) = -np₀  + np₁

P' (1) = -np_{n -1} + np_n

Hence, the slope at the starting of the curve is beside the line joining the first two control points and the slope on the ending of the curve is beside the line joining 2end-point in the last. As the same, the parametric second derivatives of a Bezier curve on the endpoints are computed as:

p' ' (0) = n)n - 1)[(p₂  - p₁ ) - (p₁ - p₀ )]

p' ' (1) = n)n - 1)[(p_{n -2}  - p_{n -1} ) - (p_{n -1} - p _n)]

The other important property of any Bezier curve is which it lies inside the convex hull as convex polygon boundary of the control points. Such follows from the properties of Bezier blending functions as: They are all +ive and their sum is all the time 1,

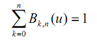
Hence any curve position is merely the weighted sum of the control-point positions. The convex-hull property for a Bezier curve makes sure about the polynomial will not have erratic oscillations.

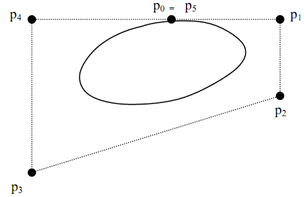
Figure (a): Shows closed Bezier curve generated by specifying the first and last control points at the same location

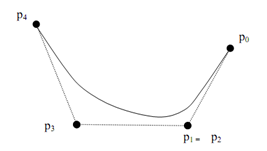
Figure(b): Demonstrates a Bezier curve can be made to pass closer to a given coordinate by assigning multiple control points to that position.