Determine the shear stress in each section - cells:

In Figure, the mean dimensions of the two cells are 100 mm × 50 mm and 50 mm square.

t₁ = 3 mm,       t₂ = 6 mm,       t₃ = 3 mm

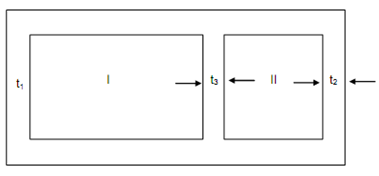
Figure

Determine the shear stress in each section, and the angle of twist per metre length for a torque of 3000 Nm. G = 80,000 N/mm².

Solution

A₁  = (100 × 50) = 5000 mm²

A₂  = 50 × 50 = 2500 mm²

Z₁  = (2 × 100) + 50 = 250 mm

Z ₂  = (2 × 50) + 50 = 150 mm

Z₃  = 50 mm

τ₁ t₁  = τ₂ t₂  + τ₃ t₃

⇒         τ₁ × 3 = τ₂ × 6 + τ₃ × 3

3 τ₁ = 6 τ₂  + 3 τ₃             ---------- (1)

T = 2 (τ₁ t₁ A₁  + τ₂ t₂ A₂ )

⇒         3000 × 10³  = 2 [τ₁ × 3 × 3000 + τ₂ × 6 × 2500]

⇒         τ₁ + τ₂  = 50            -------- (2)

(τ₁ Z₁ + τ₃ Z₃ ) / A₁ = (τ₂ Z₂ - τ₃ Z₃ )/A₂                  

 (τ₁ × 250 + τ₃ × 50) /5000= (τ₂ × 150 - τ₃ × 50)/ 2500

⇒         5 τ₁ + τ₃  = 6 τ₂  - 2 τ₃

⇒         5 τ₁ = 6 τ₂  - 3 τ₃                                           ------------ (3)

 (3) - (1) ⇒ 2 τ₁ = - 6 τ₃

τ₁ = - 3 τ₃                 ---------- (4)

From (1),

3 (- 3τ₃ ) = 6 τ₂  + 3 τ₃

τ₂  = - 2 τ₃

From (2),

- 3 τ₃  - 2 τ₃  = 50     --------- (5)

τ₃  = - 10 N/mm²

τ₁ = - 3 (- 10) = 30 N/mm²

τ₂  = - 2 (- 10) = 20 N/mm²

∴          θ= (τ₁ Z₁ + τ₃ Z₃ ) l /2G A₁ ,      Here  l = 1000 mm

= [30 × 250 + (- 10) × 50]/ (2 × 80 × 103 × 5000) × 1000

= 8.75 × 10^{- 3} radians