Average of Relatives Method
We have seen the construction of an index number using the aggregates method. In this section, we shall see the construction of an index using the average of relatives method.
Unweighted Average of Relatives Method
As usual, let us begin with a price index. When a price index is constructed, all price relatives are to be obtained for all the items included in the index after which the average of price relatives is obtained using any one of the measures of central tendency namely, arithmetic mean, geometric mean, median, mode or harmonic mean. A price relative may be generally understood as the ratio of the price of a single item in a given period to its price in the base period.
Though theoretically, any measure of central tendency can be used to obtain the index, the general practice is to use arithmetic mean for averaging the price relatives. The price index using the average of relatives method can be constructed using the following formula:
Unweighted average of relatives index |
= |
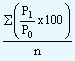 |
| |
where,
P1 = Prices in the current/given year
P0 = Prices in the base year
n = Number of products/items in the composite
The ratio P1/P0 is the price relative.
Unweighted Average of Relatives Index
|
Elements in the composite
|
Prices/Kg
|
|
|
|
|
|
Rice
|
8.50
|
9.50
|
111.76
|
|
Wheat
|
4.75
|
5.00
|
105.26
|
|
Salt
|
3.00
|
3.00
|
100.00
|
|
Sugar
|
9.00
|
11.00
|
122.22
|
|
|
|
|
439.24
|
Unweighted average of relatives price index = |
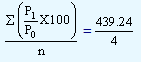 |
|
|
|
=
|
109.81 |
|
|
|
On similar lines, quantity index using average of relatives method can be computed with the help of the following formula:
| Unweighted average of relatives quantity index |
= |
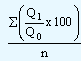 |
where,
Q1 = Quantities in the given period
Q0 = Quantities in the base year
n = Number of elements in the composite
The price index or the quantity index computed by the average of relatives method would be the same regardless of the way in which the prices are quoted or quantities are measured. In other words, price/quantity relatives are pure numbers and hence free from the units of measurement.
Also, the average of relatives method converts each element in the composite to a relative scale where each element is expressed in percentages and measured against a base of 100. The only impediment to such an index being constructed is the selection of an appropriate average. In general, arithmetic mean is used to take the average of the price relatives. As such, index is not influenced by extreme items. But the use of arithmetic mean, though simple and easy to understand, has a major disadvantage in that there is a tendency to over-emphasize increases and undervalue decreases. Though the use of geometric mean would overcome these tendencies, it is difficult to compute and its usage is avoided for this reason. The unweighted average of relatives method suffers from one or more limitations. The relatives (price/quantity) are assumed to have equal importance. As some relatives are economically more significant than others, assigning of equal weightages is undesirable.