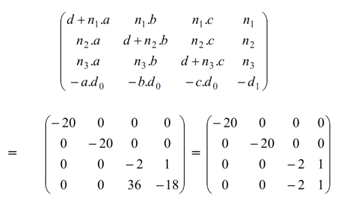Acquire the perspective transformation, Computer Graphics

Assignment Help:

Acquire the perspective transformation onto z = - 2 Plane, where (0, 0, 18) is the center of projection.

Solution: Now centre of projection, C (a, b, c) = (0, 0, 18)

∴ (n₁, n₂, n₃) = (0, 0, 1)

And Reference point is R₀ (x₀, y₀, z₀) = (0, 0, - 2)

∴ d₀ = (n₁x₀ + n₂.y₀ + n₃z₀) = - 2

d₁ = (n₁.a + n₂.b + n₃. c) = 18

We know here the general perspective transformation while cop is not at the origin is specified by:

1344_Acquire the perspective transformation.png

Related Discussions:- Acquire the perspective transformation

Explain three dimensional transformations, Explain Three Dimensional Transf...

Explain Three Dimensional Transformations A 3D geometric transformation is utilized extensively in object modelling and rendering. 2D transformations are naturally extended to

Digital painting, Please guide if there is any easy steps tutorial availabl...

Please guide if there is any easy steps tutorial available for digital painting in adobe photoshop.

Illustration of a clipping window - raster graphics, Illustration of a Clip...

Illustration of a Clipping window ABCD is placed as follows: A (100, 10), B (160, 10, C (160, 40), D (100, 40) By using Sutherland-Cohen clipping algorithm determine the vis

Mathematical description of a perspective projection, Mathematical descript...

Mathematical description of a Perspective Projection A perspective transformation is found by prescribing a center of projection and a viewing plane. Let here assume that P(x

Anti- aliasing, Anti- aliasing: Most aliasing artifacts, when appear in a ...

Anti- aliasing: Most aliasing artifacts, when appear in a static image at a moderate resolution, are often tolerable, and in many cases, negligible. However, they can have a signi

What do you understand by the term contone, Question : (a) What do you...

Question : (a) What do you understand by the term ‘contone'? (b) What are spot colours? (c) You have been asked to prepare an artwork (a magazine) to send to a printer.

Z-buffer, describe z-buffer algorithm removing hidden surface

describe z-buffer algorithm removing hidden surface

Important points about the curve segment, Important Points about the Curve ...

Important Points about the Curve segment - properties of bezier curves Note : if P (u) → = Bezier curve of sequence n and Q (u) → Bezier curve of sequence m. After that Co

Transformation, what is fixed point scaling?

what is fixed point scaling?

Types of animation systems - computer animation, Types of Animation Systems...

Types of Animation Systems - Computer Animation We have discussed above about the sequencing of animation is helpful in developing any animation. Such sequencing is more or le

Write Your Message!

Name

Email id

Message

Verfication Code

User Account

All Pages