Testing the hypothesis equality of two variances

The test for equality of two population variances is based upon the variances in two independently chosen random samples drawn from two normal populations

Beneath the null hypothesis σ₁²   =    σ₂²  

F =        (S²₁/ σ₁²)/ (S²₂/ σ₂²)    here under the H₀ :  it follows that

F =        S²₁/ S²₂ which is the test statistic.

This follows F - distribution along with V₁ and V₂ degrees of freedom. The larger sample variance is placed in the numerator and the smaller one in the denominator

If the computed value of F exceeds the table value of F, we reject the null hypothesis that is the alternate hypothesis is accepted

Illustration

In one sample of observations the sum of the squares of the deviations of the sample values from sample mean was 120 and in another sample of 12 observations it was 314. Test where the difference is significant at 5 percent level of significance

Solution

Given that n1 = 10, n2 = 12, Σ(x₁ - x¯₁ )² = 120

Σ(x₂ - x¯₂ )² = 314

Assume that take the null hypothesis that the two samples are drawn from the similar normal population of equal variance

H₀ :  s₁² = s₂²

H₁:  s₁² ≠ s₂²

Applying F test that is

F = S²₁/ S²₂

=

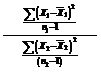
= (120/9)/(314/11)

= 13.33/28.55

As the numerator should be greater than denominator

F =  28.55/13.33 = 2.1

The table value of F at 5 percent level of significance for V₁ = 9 and V₂ = 11. Because the calculated value of F is less than the table value, we accept the hypothesis. The samples may have been drawn from the two populations having the similar variances.