Squeeze Theorem (Sandwich Theorem and the Pinching Theorem)

Assume that for all x on [a, b] (except possibly at x = c ) we have,

                                f ( x )≤ h ( x ) ≤ g ( x )

Also assume that,

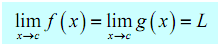
for some a ≤ c ≤ b .  Then,

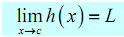
Since with the earlier fact we only have to know that f ( x ) ≤ h ( x ) ≤ g ( x ) is true around x = c .Since we are working  along with limits & they are only concerned with what is going on around x = c and not what is in fact happening at x = c .

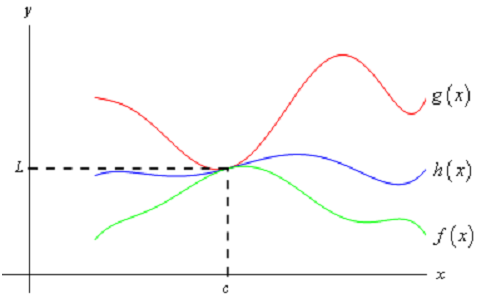
Now, if we again suppose that all three functions are nice enough (again this isn't required to make the Squeeze Theorem true, it just helps with the visualization) then we can obtain a rapid sketch of what the Squeeze Theorem is telling us. The given figure illustrates what is happening in this theorem.

From the figure we can see that if the limits of f(x) & g(x) are equal at x = c then the function values have to also be equal at x = c (it is where we're using the fact that we supposed the functions where "nice enough", that isn't really needed for the Theorem).  Though, because h(x) is "squeezed" among f(x) & g(x) at this point then h(x) ought to have the same value. Thus, the limit of h(x) at this point has to also be the same.

The Squeeze theorem is also known as the Sandwich Theorem and the Pinching Theorem. Hence, how do we employ this theorem to help us with limits?  Let's take a look at the given example to see the theorem in action.