Root of function: All throughout a calculus course we will be determining roots of functions.  A root of function is number for which the function is zero.  In other terms, determining the roots of a function, g(x), is equal to solving

                                                      g ( x ) = 0

Example: Find out all the roots of

                       f (t ) = 9t ³ -18t + + 6t

Solution :

Thus we will have to solve,

9t ³ -18t ² + 6t = 0

Firstly, we have to factor the equation as much as possible.  Doing this gives,

                                  3t (3t ² - 6t + 2) = 0

Next if a product of two things are zero then one (or both) of them must be zero. It means that,

                  3t = 0         OR,

                   3t ² - 6t +2 = 0

From the first it's apparent that one of the roots have to then be t=0. To get the remaining roots we will have to use the quadratic formula on the second equation.  Doing this gives,

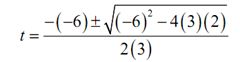
= (6±√12 )/6

= (6±√(4)(3)) /6

= (6±2√3)/6

=3±√3/3

=1±(1/3) √3

= 1±1/√3

In order to remind you how to make simpler radicals we gave various forms of the answer.

To calculate the problem, following is a complete list of all the roots of this function.

                                  t = 0, t =( 3 + √3 )/3 , t = (3 -  √3 )/3

Note we didn't employ the final form for the roots from the quadratic. It is usually where we'll stop along with the simplification for these types of roots.  Also note that, for practice, we broke up the compact form for the two roots of the quadratic.  You will have to be able to do this so ensure that you can.

This example had a couple of points other than determining roots of functions.

The first was to remind you of the quadratic formula. it won't be the last time that you'll required it

The second was to get you utilized to seeing "messy" answers.  Actually, the answers in the above list are not that messy.  Though, most of the students come out of an Algebra class very habitual to seeing only integers and the occasional "nice" fraction as answers.

Hence, here is fair warning .In "real life" (whatever that is) the answer is hardly ever a simple integer such as two.  In most of the problems the answer will be a decimal that came about from a messy fraction and/or an answer that involved radicals.