Sketch the graph of
P ( x ) = 5x5 - 20x4 + 5x3 + 50x2 - 20x - 40 .
Solution
We set up the zeroes & multiplicities of this polynomial in the previous section hence we'll just write them back down here for reference reason.
x= -1 ( multiplicity 2)
x= 2 ( multiplicity 3)
Thus, from the fact we know that x= -1 will only touch the x-axis and not in fact cross it and that x= 2 will cross the x-axis and will be flat as it does this as the multiplicity is greater than 1.
Next, the y-intercept is (0, -40) .
The coefficient of the 5th degree term is +ve and as the degree is odd we know that this polynomial will increase without any bound at the right end & decrease without any bound at the left end.
At last, we just have to evaluate the polynomial at a couple of points. The points which we pick aren't actually all that important. We just desire to pick points according to the guidelines in the procedure outlined above and points that will be rather easy to evaluate. Following are some points. We will leave it to you to check the evaluations.
P ( -2) = -320 P (1) = -20 P (3) = 80
Now, to in fact sketch the graph we'll begin on the left end & work our way across to the right end. Firstly, we know that on the left end the graph decreases without any bound as we compose x more and more negative and this agrees along with the point that we evaluated at x= -2 .
Hence, as we move to the right the function will in fact be increasing at x= -2 and we will continue to increase till we hit the first x-intercept at x= 0 . At this instance we know that the graph only touches the x-axis without really crossing it. It means at x= 0 the graph that have to be a turning point.
Now the graph is decreasing as we move to the right. Again, this agrees along with the next point which we'll run across, y-intercept.
Now, according to the next point that we've got, x= 1 , the graph ought to have another turning point somewhere among x= 0 & x= 1 as the graph is higher at x= 1 than at x= 0 . Only where this turning point will taken place is very hard to determine at this level so we won't worry regarding trying to determine it. Actually, usually determining this point needs some Calculus.
Thus, we are moving to the right & the function is increasing. The next point which we hit is the x- intercept at x= 2 & this one crosses the x-axis hence we know that there won't be a turning point here as there was at the first x-intercept. Thus, the graph will increase continually through this point till we hit the last point that we evaluated the function at, x = 3
At this instance we've hit all the x-intercepts & we know that the graph will increase without any bound at the right end and thus it looks like all we have to do is sketch in an increasing curve.
Following is a sketch of the polynomial.
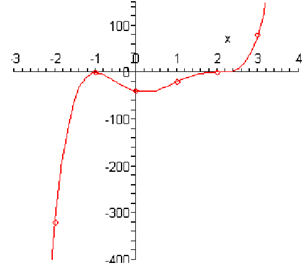
Note down that one of the causes for plotting points at the ends is to illustrates just how quick the graph is increasing or decreasing. We can illustrate from the evaluations that the graph is decreasing onto the left end much quicker than it's increasing on the right end.