Scan Conversion of Line with the slope (0 < m < 1)

Currently the pixel positions beside the line path are determined through sampling at Unit x intervals that is, starting from the first point. (x₀, y₀) of a provided line we step to all successive columns. That is x-position and plots the pixel that scan line y value is closest to the line path. Suppose we proceed in such fashion up to the k^th step. The process is demonstrated in following figure. Suppose that we have determined the pixel at (x_k, y_k). We require deciding that pixel is to be plotted in column _{xk+ 1}. Our options are either (x_{k +1}, y_k) or (x_{k + 1}, y_{k + 1}).

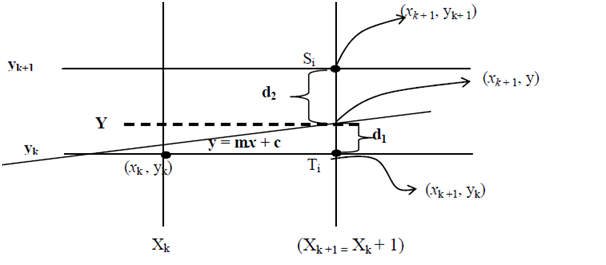
Figure: Scan conversion 0 < m < 1

On sampling position X_{k + 1} the vertical pixel or say scan line separation from mathematical line i.e. y = mx + c is say d₁ and d₂.

Currently, the y coordinate on the mathematical line on pixel column position X_{k + 1} is:

y = m (x_{k + 1}) + c                                       ---------------------(1)

By using figure of Scan conversion 0 < m < 1:

d₁ = y - y_k                                                                             ---------------------(2)

= m (xk + 1) + c - yk                                                  ---------------------(3) (by using (1))

Likewise, d₂ = (y_{k + 1}) - y = y_{k +  1} - m (x_{k + 1}) - c    ---------------------(4)

By using (3) and (4) we get d₁ - d₂

d₁ - d₂ = [m (x_{k + 1}) + c - y_k] - [y_{k + 1} - m (x_{k + 1}) - c]

= mx_k + m + c - y_k - y_{k - 1} + mx_k + m + c

= 2m (x_{k + 1}) - 2y_k + 2c - 1                     ---------------------(5)

As, decision parameter p for k^th step that is p_k is specified by

p_k   = Δx(d₁ - d₂ )---------------------(6)

Currently, a decision parameter p_k for the k^th step in the line algorithm can be acquired by rearranging (5) hence it involves merely integer calculations. To achieve this substitute m = Δy/Δx; here, Δy and Δx ⇒ vertical and horizontal separations of the ending point positions.

p_k = Δx (d₁ - d₂) = Δ x [2m (x_{k + 1}) - 2y_k + 2c - 1]

= Δx [2(Δy/Δx)  (x_{k + 1}) - 2y_k + 2c - 1]

= 2 Δy (x_{k + 1}) - 2 Δxy_k + 2 Δxc - Δx

= 2 Δy x_k - 2 Δx y_k + [2 Δy + Δx (2c - 1)]

p_k  = 2 Δy x_k - 2Δxy_k + b               -------------------- (7)

Here b is constant with value b = 2Δy + Δx (2c - 1)       ---------------------(8)

Note: sign of p_k is as similar as sign of d₁ - d₂ as it is assumed like Δx > 0; here in figure of Scan conversion 0 < m < 1 , d₁ < d₂ i.e. (d1 - d2) is -ve that is , p_k is negative so pixel T_i is more suitable option otherwise pixel S_i is the proper option.

That is (1) if p_k < 0 choose T_i, hence subsequent pixel option (x_k, y_k) is (x_{k + 1}, y_k) else (2) if p_k > 0 decide S_i, so subsequent pixel option after (x_k , y_k ) is (x_{k + 1}, y_{k + 1}).

At step k + 1 the decision parameter is evaluated via writing (7) as:

p_{k + 1} = 2Δy x_{k + 1} - 2Δx y_{k + 1}   + b         ---------------------(9)

Subtracting (7) from (9) we find:

Such recursive calculation of decision parameter is preformed at all integer positions, starting along with the left coordinate ending point of line.

This first parameter p₀ is calculated by utilizing Eq(7), and (8) at the beginning pixel position (x₀, y₀) along with m evaluated as Δy /Δx (that is intercept c = 0)

p₀ = 0 - 0 + b = 2Δy + Δx (2 * 0 - 1) = 2Δy - Δx

p₀ = 2Δy - Δx                                           -----------------------(10 A)