Logarithmic Differentiation : There is one final topic to discuss in this section. Taking derivatives of some complicated functions can be simplified by using logarithms.  It is called logarithmic differentiation.

It's easiest to illustrate how this works in an example.

Example Differentiate the function.

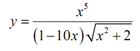
Solution: Differentiating this function could be completed with a product rule & quotient rule. Though, that would be a fairly messy procedure. We can make simpler things somewhat by taking logarithms of both sides.

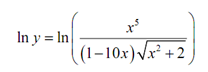
Certainly, it isn't really simpler.  What we have to do is utilize the properties of logarithms to expand the right side as follows.

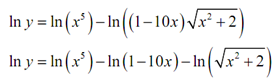
It doesn't look all that simple.  Though, the differentiation procedure will be simpler.  What we have to do at this point is differentiate both of the sides w.r.t x.  Note as well that it is really implicit differentiation.

y′ /y= 5x⁴ / x⁵ = -10/(1-10x) - ((1/2)   (x²+2)^(-1/2)(2x)/(x²+2)^(1/2)

y′ /y= 5/ x +10/(1-10x) - x/ (x²+2)

To finish the problem all that we have to do is multiply both sides through y and the plug in for y as we do know what that is.

y′ = y ( 5/x +   (10/1 -10 x)    - x/ x² + 2))    

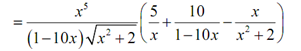
Based upon the person, doing this would perhaps be slightly easier than doing both the quotient & product rule. The answer is approximately definitely simpler than what we would have gotten by using the product & quotient rule.

We can also utilize logarithmic differentiation to differentiation functions in the form.

                                    y = ( f ( x ))^{g ( x )}