Important Points about the Curve segment - properties of bezier curves

Note: if P (u) → = Bezier curve of sequence n and Q (u) → Bezier curve of sequence m.

After that Continuities in between P(u) and Q(u) are as:

1)      Positional continuity of 2 curves

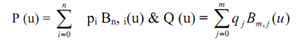
That is p_n = q₀

2)       C¹ continuity of 2 curve P (u) and Q (u) as that point p_{n - 1}, p_n on curve P(u) and q₀, q₁ points upon curve Q(u) are collinear that is:

n( p_n  - p_n-1 ) = m(q₁ - q₀ )

n q₁  = q₀  +( p_n  - p_{n -1} ).(n/m)

 ⇒ (d p/du)_u=1         =  (d q/dv)_v=0

G⁽¹⁾  continuity of two curves P(u) and Q(u) at the joining that are the end of P(u) along with the beginning of q(u) as:

p_n  = q₀n( p_n  - p_{n -1} ) = kn(q₁  - q₀ ),

Here k is a constant and k > 0

⇒ p_{n -1} , p_­  = q₀ , q₁  are collinear

3)  c2 continuity is:

a)   C⁽¹⁾ continuity

b)   m (m - 1) (q₀ - 2q₁ + q₂)

= n (n - 1) (p_n - 2p_{n - 1} + p_{n - 2})

That points are as: p_{n - 2}, p_{n - 1}, p_n of P(u) and points q₀ , q₁, q₂ of Q(u) should  be collinear further we can verify whether both second and first order derivatives of two curve sections are similar at the intersection or not  that is:

(d p)/( d u) _u=1  =   (d q) /(d v )_v=0

And (d² p)/( d u²) _u=1  =   (d² q) /(d v² )_v=0

Whether they are similar we can as we have C² continuity   

 Note: as the same we can explain higher order parametric continuities