Important Points About the Alternating Series Test
There are a several things to note about this test. Very first, unlike the Integral Test and the Comparison or Limit Comparison Test, this test will just only tell us while a series converges and not if a series will diverge.
After that 2nd, in the second state all that we need to require is that the series terms, bn will be eventually decreasing. It is probable for the first few terms of a series to raise and still have the test be valid. All that is needed is that eventually we will have bn ≥ bn+1 for all n later than some point.
To observe why this is consider the subsequent series,
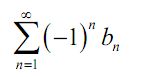
Let us assume that for 1<n<N {bn} is not decreasing and that for n > N+1 {bn} is decreasing. The series can be written like:
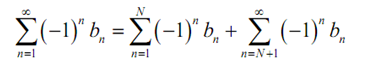
Here the first series is a finite sum there is no matter how large N is of finite terms and thus we can calculate its value and it will be finite. The convergence of this series will depend upon only on the convergence of the second that is infinite series. If the 2nd series has a finite value as compared to the sum of two finite values is as well finite and thus the original series will converge to a finite value. Alternatively if the second series is divergent either as its value is infinite or it doesn't have a value after that adding a finite number onto this will not change that fact and thus the original series will be divergent.
The point of all this is that we do not need to require that the series terms be decreasing for each n. We just only need to require that the series terms will eventually be decreasing as we can all time strip out the first few terms that aren't in fact decreasing and look only at the terms which are actually decreasing.
Note: in reality, we don't actually strip out the terms which aren't decreasing. All we do is test that eventually the series terms are decreasing and after that apply the test.