We are until now going to suppose that there will be no external forces acting on the system, along with the exception of damping obviously. Under this case the differential equation will be as

mu′′ + g u′ + ku = 0

Here m, g, and k are all positive constants. By solving this for the roots of the characteristic equation we determine the following,

r_1,2 = (- g+√( g² - 4mk))/2m

We will have three cases now.

1.      g² - 4mk = 0

Under this case we will find a double root out of the characteristic equation and the displacement at any time t will be as,

u(t) = c₁e^-((gt)/(2m)) = c₂te^-((gt)/(2m))

Make sure that as t → ∞ the displacement will approach zero and therefore the damping under this case will do what it's supposed to do.

This case is termed as critical damping and will occur when the damping coefficient is,

g² - 4mk = 0

g² = 4mk

g = 2√(mk) = g_CR

The value of the damping coefficient that gives critical damping is called the critical damping coefficient and denoted by ?CR.

2.      g² - 4mk > 0

Under this case let's rewrite the roots a little.

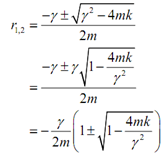
Also see that from our initial assumption which we have,

g² > 4 mk

1 > (4mk)/ g²

By using this we can notice that the fraction in the square root above is less than one. So if the quantity under the square root is less than one, it implies that the square root of this quantity is also going to be less than one. Conversely,

√(1 - (4mk)/ g²) < 1

Why is this significant? Well, the quantity in the parenthesis is now one minus/plus a number which is less than one. It means that the quantity in the parenthesis is guaranteed to be positive and therefore the two roots under this case are guaranteed to be negative.  Thus the displacement at any time t is,

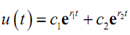
And will approach zero as t → ∞. Therefore, once again the damper does what this is supposed to do.

This case will arise when,

g² > 4mk

g²  > 2√(mk)

g > g_CR

And this is termed as over damping.

3.      g 2 - 4mk < 0

Under this case we will find complex roots out of the characteristic equation.

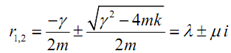
Here the real part is guaranteed to be negative and therefore the displacement is as

U(t) = c₁e^lt cos(µt) + c₂ e^lt sin(µt)

= e^lt (c₁ cos(µt) + c₂ sin(µt))

= R e^lt(cos(ut - d))

Make sure that we reduced the sine and cosine down to a single cosine under this case as we did in the undamped case.  Also, as l < 0 the displacement will move toward zero as t → ∞ and the damper will also work as it's assumed to in this case.

 We will find this case will arise when,

g² < 4mk

g²  < 2√(mk)

g < g_CR

This is termed as under damping.