Evaluate the following integral.

∫√(x²+4x+5) dx

Solution:

Remind from the Trig Substitution section that to do a trig substitution here we first required to complete the square on the quadratic. This provides,

X²+4x+5 = x2+4x+4-4+5=(x+2)²+1

After completing the square the integral becomes like this:

∫√(x² + 4x +5) dx

= ∫ √ ((x+2)² 1dx)

Upon doing this we can recognize the trig substitution that we require.  Here it is,

x + 2 = tan θ

x= tan θ -2

dx = sec² θdθ

√((x + 2)² +1)

= √ tan² θ+1

=√ sec² θ

=|sec θ |

= sec θ

Recall that as we are doing an indefinite integral we be able to drop the absolute value bars.  By using this substitution the integral becomes,

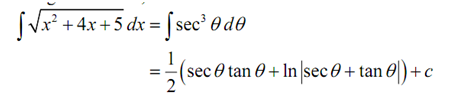
∫ √x² + 4x + 5 dx = ∫ sec³ θ d θ

= ½ (secθ tanθ + ln |secθ + tan θ|) + c

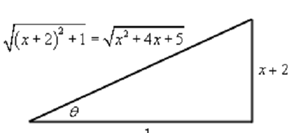
We can end the integral out along with the following right triangle.

tanθ = (x+2/1)

secθ = √(x² + 4x +5/1)

        = √ (x²+4x+5)

∫ √(x²+4x+5) dx = ½ ((x+2)√x²+4x+5+1n|x+2+√x²+4x+5|) + c

Thus, by completing the square we were capable to take an integral that had a general quadratic in it and transform it into a form that permitted us to make use of a known integration technique.