Derive the common transformation of parallel projection into the xy-plane in the direction of projection d=aI+bJ+cK.

Solution: The common transformation of parallel projection into the xy-plane towards the projection d=aI+bJ+cK, is derived as follows in the figure a:

Assume here that P(x,y,z) be an object point, projected to P'(x',y',z') into the z'=0 plane. By figure (a) we observe that the vectors d and PP' have the similar direction. It implies that:

PP'=k.d , comparing part, we find that:

x'-x=k.a

y'-y=k.b

z'-z=k.c

As like z'=0 on the projection plane, we obtain k=-z/c. As,

x'=x-a.z/c

y'=y-b.z/c

 z'=0    

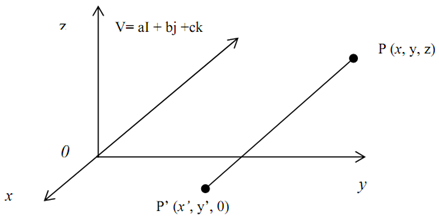
Figure: (a)

In terms of coordinates of homogeneous, so this equation can be become as:

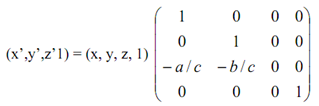
It is,  P'_h =P_h.P_par,z , here Ppar,z  is the parallel projection along with the direction of projection d along the unit vector k.