Analyse the state of stress at the critical section:
A prismatic bar of circular section with 80 mm diameter is subjected to bending moment of 5 kN-m and a torque of 7 kN-m. Analyse the state of stress at the critical section.
Solution
Moment of the inertia, I = πD4/64 = π×804/64 = 2.016×106 mm4
Polar moment of inertia, J = πD4/32 = π/32 ×804 = 4.032×106 mm4
Maximum bending stress, σx = Mymax/I = 5×106×40/2.016×106 = 99.206 N/mm2
Maximum shear stress τxy = 7 × 106 × 40/4.032×106 =69.444 N/mm2
Determination of Principal Stress
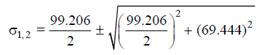
Thus, we get
σ1 = 134.944 N/mm2 and σ2 = -35.737 N/mm2
τmax =σ1 -σ 2/2 = 85.34 N/mm2
Note
While the cross-section of the bar is hollow circular along with outer and inner diameters D and d respectively the analysis of stresses is to be carried through the similar procedure except for using the expressions,
I = π/64 (D4 -d4) and J =π/32 (D4 -d4)