Reference no: EM133209771

Managing Operations

Question 1. Consider the following process. For each station, p is the average process time (days), m is the number of servers, and Rp is the total capacity rate of each station (unit/day). Assume that the final assembly (Station 4) requires one part from Path 1 and one part from Path 2 to complete one finished product.

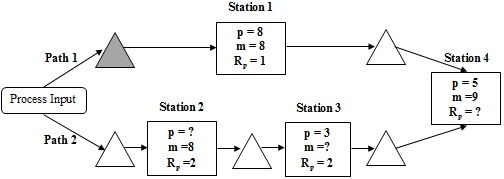
a) Fill out the unknowns in the process flow diagram:

b) What is the theoretical flow time of completing the entire process? Justify your answer.

c) What is the maximum possible rate of production that this system can achieve under the current configuration? Justify your answer.

d) If 0.9 parts are released into both paths every day for processing, what is the (actual) utilization of each station?

e) Suppose that jobs are released to Station 1 at the rate of 0.9 parts per day, and the inter-arrival time distribution has a coefficient of variation CVa = 1. The coefficient of variation for Station 1's processing time equals CVp = 1. Compute the average delay that a job would experience at Station 1 and the average number of units in the highlighted buffer (the one before Station 1).

f) You have been told that your task is to increase the capacity rate of the whole system to 1.2 units per day while decreasing the total number of servers in the system. How would you accomplish this? How many servers would you have at each station?

Question 2. An insulation plant makes two types of insulation called type B and type R. Both types of insulation are produced using the same machine. The machine can produce any mix of output, as long as the total weight is no more than 70 tons per day. Insulation leaves the plant in trucks; the loading facilities can handle up to 30 trucks per day. One truckload of type B insulation weighs 1.4 tons; one truckload of type R weighs 2.8 tons. Each truck can carry type B insulation, type R insulation, or any mixture thereof. The insulation contains a flame retarding agent which is presently in short supply; the plant can obtain at most 65 canisters of the agent per day. One truckload of (finished) type B insulation requires an input of three canisters of the agent, but one truckload of type R insulation requires only one canister.

Carla Linton, the plant manager, has calculated that, at current prices, the contribution from each truckload of type B is $950, and $1,200 for type R. There appears to be no difficulty in selling the entire output of the plant, no matter what production mix is selected. How much of each kind of insulation should be produced? Formulate the problem of determining the optimal number of truckloads of types B and R and use the Excel Solver to obtain a solution.

Question 3. Kristen orders paper take-out bags with her logo printed on them. Kristen decides to optimize the inventory policy for take-out bags using what she learned from the OM class. Daily demand for take-out bags is normally distributed with a mean of 75 bags and a standard deviation of 25 bags. Kristen's printer charges her $10 per order for print setup independent of order size. Bags are printed in batches of 100, and priced at $5 per batch (i.e., 5 cents each bag). It takes 5 days for an order to be printed and delivered. The only holding cost is the opportunity cost of capital, which is estimated to be 30% per year. Assume 360 days per year.
a) What is the optimal order quantity per order for Kristen?

b) If Kristen wants to make sure the bags do not run out with 99% probability during the order lead time, what is her optimal reorder point?

c) Using the above ordering strategy, on average how often will Kristen's bag inventory run out (circle one)? (If Kristen stocks out for multiple consecutive days, it counts as one stockout incident.)
(1) Once every 100 days (2) Once every 400 days
(3) Once every 3 years (4) Once every 22 years

d) How long on average does each bag spend in Kristen's kitchen?

Question 4. The Silky Shirts Company based in Thailand makes silk women's shirts for a retailer in the U.S. It costs Silky $30 to make each shirt. Silky sells them to the retailer for $50 and the shirts retail for $100. The retailer estimates that it can sell an average of 800 shirts with a standard deviation of 400 at this price per season (normally distributed). The retailer sells all remaining shirts for $20 at the end of the season.

a) How many shirts should the retailer order to maximize its own profit?

b) If Silky had its own stores, and could make and sell (at the same retail price as above) its own shirts in its own stores instead of needing the retailer as a middleman, how many shirts would it order assuming demand remained the same as above?

c) Silky wants to induce the retailer to order as many shirts as the integrated company would order in Part b). One strategy that Silky is considering is to offer a "buy-back" contract to the retailer, in which case Silky will purchase back any unsold shirts by the end of the season (the retailer no longer sells the remaining shirts by itself). At what price would Silky have to buy back the unsold shirts to induce the retailer to order as many shirts as the integrated company would order in Part b)?

Question 5. All patients who arrive to the Emergency Department (ED) of Cleanland Clinic first go to Registration and then to Triage. Triage is staffed by two nurses. Triage is considering creating two separate lines, the first for patients with surnames starting with a letter in the range A-M, the second for N-Z. Each line would have a Triage nurse dedicated to serve only that line of patients. Assume that the average patient arrival rates to each line would be roughly the same. What effect do you think creating these dedicated lines will have on the average waiting time experienced by patients at Triage? Will the waiting time increase, decrease, or remain the same? Justify your answer.
A: ¿
B: ?

Question 6. What is the bullwhip effect? How can Vendor Managed Inventory help mitigate the bullwhip effect?

Question 7. a) Toyota uses the Andon system to (circle one):
(1) level or balance the production
(2) make mistakes known
(3) reduce setup times
(4) achieve just-in-time production
(5) manage relationships with suppliers

b) The Toyota Production System has received much acclaim for how well it can cut costs and improve quality in a manufacturing environment. Judge whether the followings contribute to its success. Circle Yes or No for each item.
Yes No Use large batch sizes to cut costs through economies of scale
Yes No Use leveled production (heijunka) to reduce inventory and idle time for workers and machines
Yes No Use mechanical jidoka (automation) to eliminate the need for operators to watch over each machine continuously
Yes No Eliminate all work in process inventories to minimize holding costs

b) Provide a real-life, or everyday, example of poka-yoke.