Plot the belief of robot distribution after each step

Assignment Help MATLAB Programming

Reference no: EM132274221

Problem - 24h take home portion

This problem must represent your own work. No collaboration or discussion with others is allowed. Other resources (class notes, homeworks, etc.) are allowed. Your submission must be received by 11:59p on Tuesday, April 2nd. You are to upload your files directly to the Gradescope website as two attachments: 1. A .tar.gz or .zip file containing a directory named after your uniqname that includes the code, 2. A PDF with the summary report of the results including figures and discussion.

A 2-D world is divided into a 100m x 100m grid (discretized in blocks of 1m²). There is a wall at the South end of the grid. The robot has a sensor that can measure the distance to the wall. The robot also has a sensor that can measure the distance to a beacon at (75, 75). Both these measurement models have a triangle probability density. The range of uncertainty is 10m for the wall sensor and 5m for the beacon sensor. The motion model also has a triangular uncertainty around the odometry obtained. This has a range of 15m.

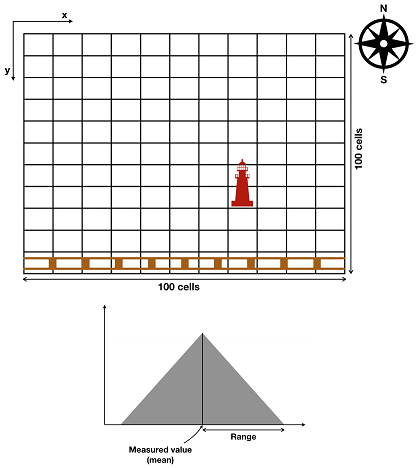
The initial position of the robot on the grid is unknown. The robot takes the following steps:

1. Move to the East for a distance of 30m.

2. Measure distance to the wall. Reading is 70m.

3. Move to the South for a distance of 10m.

4. Measure distance to the beacon. Reading is 30m.

Program the problem in MATLAB and plot the belief of robot distribution after each step. To plot the belief, you can plot a gray-scale image of 100m x 100m pixels.

Reference no: EM132274221

Questions Cloud

Do you want to work for Google : Do you want to work for Google? Do you think you are a smart creative?

What is jurisdiction : What is jurisdiction? Explain the different types of jurisdiction outlined in the book and explain under what circumstances a federal court

Describe the importance of employee benefits : Describe the importance of employee benefits as a strategic component of fulfilling the goals of HRM at Genentech and Zappos?

What is the role of critical thinking in daily life : What is an example of a situation in which you can utilize critical thinking in your own life, and how can critical thinking help in this situation?

Plot the belief of robot distribution after each step : Problem - 24h take home portion. Program the problem in MATLAB and plot the belief of robot distribution after each step

Labour productivity before and after the improvement : Calculate the labour productivity before and after the improvement, and the percentage of increase

Deciding on the organizational culture : If you were going to run a business with a family member, how would you go about deciding on the organizational culture you want to create?

Why is this issue important : Choose an issue that the Coca Cola company should be focused. Why is this issue important? Please support this issue with more information.

What are customer value-satisfaction and loyalty : What are customer value, satisfaction, and loyalty, and how can companies deliver each of them? Use Panera Bread to illustrate those concepts

User Account

All Pages