Reference no: EM13885

1. Let p_n(x) be the Lagrange interpolating polynomial of degree at most n that satis?es p_n(x_i) = y_i, i = 0, 1, 2, . . . , n.
Write a MATLAB function to evaluate pn at a set of points stored in the MATLAB vector z. Assuming the points x₀, x₁, . . . , x_n are stored in the MATLAB vector x and the values y₀, y₁, . . . , y_n are stored in the MATLAB vector y, the input to your function should be x, y and z. The output should be a vector, of the same length as z, containing the values of the polynomial at the points stored in z.

2. Use your MATLAB function to compute the Lagrange interpolating polynomial of degree at most n for the function f(x) = ln(x + 1) on the interval [0, 2], with uniformly distributed interpolation points, for n = 1 and n = 2. For each value of n, produce a plot containing the
interpolation points, the function f(x) and the polynomial pn(x) for x 2 [0, 2], when ploting f(x) and pn(x), you should use a vector z containing 500 uniformly distributed points in the interval [0, 2].

3. Consider the interpolation error for the function f of Question 2 e_n(x) = |f(x) - pn(x)|, n = 0, 1, . . .
Produce a plot showing that e₂(x) ≤ e₁(x) in the interval [0, 2].

4. Calculate an approximation to the in?nity norm of the error in the Lagrange interpolating polynomials p_n(x) of the function f(x) for n = 1, 2, . . . , 10.

5. Repeat question 4 for the function g(x) = f(10x) = ln(10x + 1).

6. Let h be the function de?ned by h(x) = ln(x + 1), with  > 0. Prove by induction that the nth derivative of h is given by

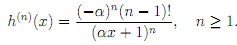
7. Read the documentation of the MATLAB command semilogy, which plots data with a logarithmic scale for the y-axis. Use semilogy to plot, on the same graph, the in?nity norm of the error against n for the functions f(x) and g(x). Explain the plot using the result of Question 6.