Find a simpler DNF equivalent

Assignment Help Theory of Computation

Reference no: EM132505488

Question 1: This question is about tableaus. You may use either tree-like tableaus, or queue-like tableaus.

a. For each of the following propositional formulas, make and expand a tableau with the formula at the root. Use your tableau to state whether the formula is satisfiable or not. In each case find a DNF formula equivalent to the given formula. Find a simpler DNF equivalent if possible.

1. ((p V q) A (¬p V ¬q)
2. ¬((p → q) → p)
3. (((p Λ ¬q) V (¬p Λ q)) → ((p V q) Λ (¬p V ¬q)))
4. ((p → q) A (q → p)).

b. For each of the following propositional formulas, make and expand a tableau with a suitable formula at the root and use it to find a formula in conjunctive normal form (CNF) equivalent to the given formula.
1. ¬((p V q) → (p Λ q))
2. (¬(p → q) V ¬(q →. p))
3. (¬(p → q) V ¬(q → r)).

c. Let L be the first-order language with no function symbols, no constants, four unary predicates P,Q,R,S and one binary predicate B. For each of the following first order formulas, define a suitable tableau to determine whether the formula is valid or not. If the formula is not valid, use your tableau to define a structure where the formula fails to hold.

1. ∀x((P (x) V ∀y(P(y) Λ ¬∀zB(y, z))))
2. ¬(∃xP(x) Λ ∀x(P (x) → ∃yP(y))
3. ((∀x((P (x) Λ Q (x)) → R(x)) Λ ¬∃x(S(x) Λ R(x))) → ∀x((P (x) Λ Q (x)) → ¬S(x)))

Question 2. a. Consider a Kripke frame F = ({x, y, z}, {(x, x), (x, (y, (y, z), (z, x)}) and a valuation u where v (p) = {x, y}, v(q) = {x, z} shown below.

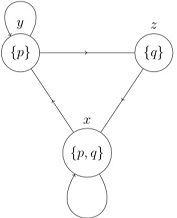
For each formula 0 below, write all worlds ω ∈ {x, y, z} for which F, v, ω |= Φ

1. p Λ ¬q Λ ◊q
2. ◊(q Λ ◊(p Λ q).
3. ◊(p → ◊p)

b. Define what it means when we say that f : F → G; is a a p-inorphisin from Kripke frame F to Kripke frame G.

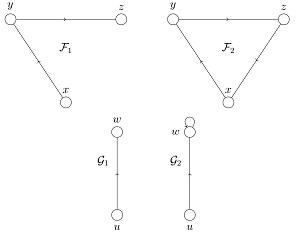
c. Consider the Kripke frames (shown below)
F1 = ({x, y, z}, {(x, y), (y, Z)}), F2 = ({X) y, z}, {(x, y), (y, z), (z, x)}) and
G1 = (u, w}, {(u, w)}, G2 = ({u, v}, {(u, w), (w, w)}).

For which i, j ∈ {1, 2} is there a frame p-morphism from ri to gi? In each case either define a p-morphism or explain why there is no p-morphism.

d. A Kripke frame (V, E) is symmetric if (x, y) ∈ E → (y, x) ∈ E. Define a modal formula that is valid in a Kripke frame if and only if the Kripke frame is symmetric. Prove that your formula is valid over symmetric frames but not valid over any other frames.

Reference no: EM132505488

Questions Cloud

Compute the value of this stock price in five years : Compute the value of this stock price in five years. Calculate the present value of these cash flows using an 8 percent discount rate.

Why is the use of a single activity base : Explain how activity-based costing can improve overhead cost allocation in companies that produce a diverse line of products. Why is use of a single activity

What is decrease to be recorded in the income statement : If provision for doubtful debts is maintained at 5%, what is the increase/decrease to be recorded in the income statement? Current provision for doubtful debts

Complete the effective interest rate amortization table : Prepare journal entries to record the issuance of the bonds on October 1, 2018, required for April 1, 2019 transactions regarding this bond issue

Find a simpler DNF equivalent : Make and expand a tableau with the formula at the root - Find a simpler DNF equivalent if possible - For each of the following propositional formulas

What journal entry would be made at the date of retirement : What would the balance sheet section for bonds look like after retirement of the bonds? What journal entry would be made at the date of retirement?

Calculate the total dividends to be paid to each group : Calculate the total dividends to be paid to each group of shareholders in each year by completing the following chart. Assume that the preferred shares

Graphically represent the business cycle : Assume you own a new car dealership. Graphically represent the business cycle and reflect on which phase(s) of a business cycle will your car sales

Demand and supply of so many goods in the economy : Illustrate with well labelled graphs, how the minimum wage affects demand, supply and equilibrium.

User Account

All Pages