Reference no: EM13768
1.
Let s1 and s2 be two strings of lengths m and n respectively. By de?nition, a superstring of s1 and s2 is one which contains s1 and s2 as substrings. Give a dynamic programming algorithm to compute a shortest superstring of two strings, and analyze its complexity.
Example: If s1 = aaaagatacac and s2 = acacggtttt then the following are all valid superstrings:
{aaaagatacacggtttt, aaaagatacacacggtttt, aaaagatacacacacggtttt}
However, aaaagatacacggtttt is the shortest. Note that the above formulation does not allow any variations (mismatches or gaps) within the overlapping region.
The motivating application for this problem is genome assembly, where the goal is to reconstruct an unknown supersequence by assembling smaller (known) fragments obtained from it.
2. Give a dynamic programming algorithm for the problem of ?nding an optimal local alignment between a string and itself - ie., we wish to ?nd a pair of best aligning substrings within s.
Note that we cannot directly use the Smith-Waterman local alignment algorithm because it will then only output the entire string aligned to itself as its ?nal answer, which is not the answer we want here. We are after a pair of shorter substrings within s. To make this routine more biologically relevant, you can assume that any optimally aligning pair of substrings that your algorithm detects should NOT overlap within the string - i.e., your optimal local alignment should correspond to two substrings s[i1 . . . i2] and s[j1 . . . j2], such that i2 < j1 (without loss of generality).
The motivating application for this problem is to ?nd "genomic repeats", which are repetitive substrings (with a few variations) present in different loci along a long genome.
3.
How will you modify the linear space Hirschberg technique to work for optimal local alignment computation in linear space (both opt. local alignment score & traceback path)? Explain the main steps of your new (modi?ed) algorithm. No need to expand on parts that are identical to the version of the algorithm discussed for global alignment computation in class.
4.
A q-gram1 is de?ned as a string of length q, where q > 0 is a "small" constant (say, q < 10). Given a string s, let Qq s denote the set of all q-grams in s. Given two strings s1 and s2 of lengths m and n respectively, their q-gram distance is the sum of the number of unique q-grams in each - i.e., qd(s1, s2) = |Qq s1\Qq s2 | + |Qq s2\Qq s1
(Note: the pipe symbol '|' in this expression stands for set cardinality - not absolute values; also the \ symbol stands for set difference.)
a) Give an algorithm to compute qd(s1, s2).
b) Derive a tight lower-bound for edit distance between two strings as a function of their q-gram distance.
c) Using the above results, argue how we can save time in practice in the following scenario: we are interesting in knowing the (optimal) edit distance between two strings only if it is below a certain cutoff, say τ . Otherwise, we don't care what is output.
5.
Given a pattern P of length m and a text T of length n, give an algorithm to ?nd and report all occurrences of P in T using the look-up table data-structure. You can assume that n > m > k, where k is the window length used to build the lookup table.
6.
The nested pairing problem:
Let s be a DNA sequence of length n, as illustrated in Figure 1. We de?ne "pairing" as a set of disjoint pairs of indices in s. A pairing is "proper" only if it is one of the following four pairs: {(a, t), (t, a), (c, g), (g, c)}. Any proper pairing becomes a "nested pairing" when the
string index intervals covered by no two pairs overlap. Put another way with reference to the Figure 1, no two edges should criss-cross.
The problem for this question is to ?nd an optimal nested pairing - i.e., a nested pairing with maximum cardinality.
Give an e?cient algorithm to compute an optimal nested pairing using dynamic programming and comment on its runtime and space requirements.
PS: As a reference, my solution for this problem takes O(n3) time.
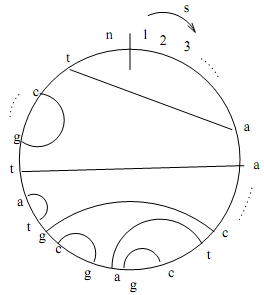
Figure: Illustration of a nested pairing of a string s of length n. Each pair is shown as an edge connecting those two character locations along the string. Note that the sequence shown s is *not* a circular string, as the start index (1) and end index (n) are clearly marked. It is only shown as circular for ease of illustrating the nested pairing.