Reference no: EM132210171

In this assignment, we develop a quadrature method for computing _-1∫¹ g(x) √(1 - x²)dx for a given g : [-1, 1] → R. You can use the built-in routines to compare your results and compute errors for use in §B.

A1. Show that p₀(x) = 1 and p₁(x) = 2x . By using a trigonometric identity, show that

p_n(x) = 2xp_n-1(x) - p_n-2(x), n = 2, 3, .....

Hence, show that p_n(x) is a polynomial of degree n and that p₀,......, p_n form a basis for p_n.

A2. Let x₁, ......., x_n denote the roots of p_n(x) . Show that the matrix

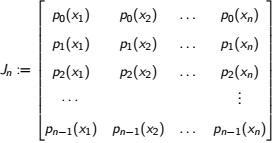
is non-singular. Hence, show that there exist w₁, ..... w_n, such that

HINT: Suppose that there exists a c 2 Rn such that c TJn = 0 .

A3. By making a substitution, show that

_-1∫¹ p_n(x)p_m(x)√(1 - x²)dx = 0, n ≠ m

A4. By using the basis {p₀, .....}, for p_n for pn and A3, prove that

_-1∫¹ p(x)√(1 - x²)dx = Σ_i=1ⁿ p(x_i)w_i,  ∀p∈p_n,

for the x_i and w_i defined above.

Now show that the relationship also holds for p∈p_2n-1 to show the quadrature rule has degree of precision at least 2n - 1 and hence is a Gaussian quadrature rule.

A5. Let q₀(x) := 1 and q_n(x) := 2ⁿdet(xl - A_n) for n = 1, 2, : : : , where A_n is the n × n matrix

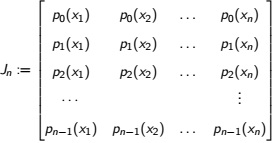
Show that q_n = p_n for n = 1, 2, : : : .

Hence, show that eigenvalues of An equal the quadrature nodes x_i.

A6. Denote the ith column of J_n (from A2) by

vⁱ = [p₀(x_i), p₁(x_i),........pn-1(x_i)]^T , i = 1.....n

Show that vⁱ is an eigenvector of A_n corresponding to the eigenvalue x_i. Hence, show that the quadrature weight

w_i = A.(1/||vⁱ||²) (vⁱ₁)² , A :=  _-1∫¹√(1 - x²)dx = 1/2Π

where v₁ⁱ  is the first component of the ith eigenvector vⁱ.

B Computing

B1. Write a MATLAB code to compute the quadrature nodes x₁, ....... , x_n and weights w₁, ....., w_n for the quadrature rule developed in §A.

Fill in
function [x,w]=getquad(n)%
% Return a vector of quadrature nodes x and weights w,
% of dimension n.
% ....

B2. Write a routine to evaluate the quadrature for a given function g . Fill in function out=myquad(g,x,w)%
% Evaluate sum_{i=1,...,n} w_i g(x_i)
assert (length(x)==length(w)) % error checking
%...
%...
out= % give return value

It should run with the call
myquad(@(x) x,x,w)
to evaluate _-1∫¹x√(1 - x²)dx. Verify the degree of precision is 2n - 1 for n = 10 (using MATLAB).

B3. Use the built-in MATLAB routines to find reference values for

_-1∫¹g(x)√(1 - x²)dx

in the case g₁(x) = exp(x) and g₂(x) = x sin(x) . We use these values in the next question to evaluate error. Note down the number of function evaluations, when using quad.

B4. Using the quadrature method developed in B2., evaluate

_-1∫¹g_i(x)√(1 - x²)dx,  for  i = 1,2

Give a plot of the error against n , taking care to use an appropriate range of n and plot (e.g., loglog vs plot vs semilogx etc).

Compare the number of function evaluations used by the MATLAB routine quad and the method of B2.