Reference no: EM132636837

CS 317 Automata and Formal Languages - Washington State University

Pay attention to writing all the steps of a proof.

Question 1. For Σ = {a, b}, construct two NFAs, one accepting the language A and one

accepting the language B. (Notes, since every DFA is also an NFA, you can make a DFA if you want.)

a. A = {w | w is in Σ* and w has an odd number of a's}

b. B = {w | w is in Σ* and w ends in ab}

c. Construct an NFA (use ε) for the language L = {w | w is in A or w is in B}

Question 2. Give state diagrams for NFAs that have the specified number of states and recognize the following languages where Σ = {1, 0}.

a. L = {w | w is in Σ* and w contains the substring 0101 so w = x0101y for some x, y} using only 5 states

b. L = {w | w is in Σ* and w contains an even number of 0's or contains exactly two 1's} using only 6 states

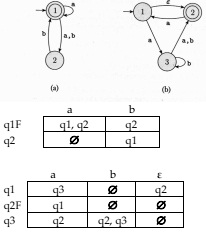
Question 3. Use the construction given in Theorem 1.39 to convert the following two nondeterministic finite automata to equivalent deterministic finite automata. The start state is q1.

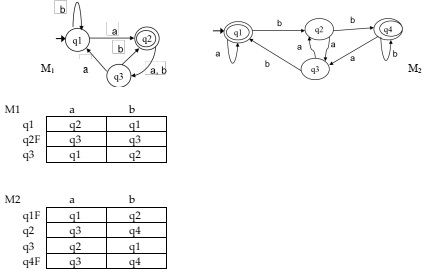
Question 4. For each of the DFAs M₁ and M₂ pictured below, using the construction given in Theorem 1.49 on page 62, make two new NFAs that accept the languages A* and B* where A = L(M₁) and B = L(M₂).

Question 5. Give regular expressions (using Σ = {a, b}, ε, Φ and the operators U, °, *) for the following subsets of {a, b}*.

a. A = {w | w begins with bb and ends with aa}

b. B = {w | w has an odd number of b's}

c. C = {w | w has an even number of a's and an even number of b's}

d. D = {w | w contains at least two a's and at most one b}

Question 6. Use the procedure described in Lemma 1.55 (If a language is described by a regular expression, then it is regular.) to construct NFAs that accept the sets of strings matching the following regular expressions. Σ = {0, 1}.

a. (000 U 11*)*

b. (000)*1 U (00)*1

Question 7. For Σ = {a, b}, construct NFAs that accept the set of strings matching the following regular expressions. You do not need to use the method in Lemma 1.55.

a. a(abb)* U a+(ε U b)

b. (ab)* U (a U b(ab*a)*b)*

Question 8. Give the regular expression for the FA {{q1, q2}, S = {a, b}, d, q1, {q1}}.

	a	b
q1 F	q1	q2
q2	q1	q2

Question 9. Give a regular expression for the FA {{q1, q2, q3, q4}, S = {a, b}, d, q1, {q3}}.

d	a	b
q1	q2	q4
q2	q3	q2
q3 F	q4	q3
q4	q4	q4

Question 10. Give a regular expression for the FA {{q1, q2, q3}, S = {a, b}, d, q1, {q2, q3}}.

d	a	b
q1	q2	q3
q2 F	q1	q2
q3 F	q1	q3