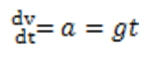Reference no: EM13332396
The future-value-of-money formula relates how much a current investment will be worth in the future, assuming a constant interest rate.
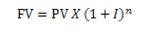
where
FV is the future value
PV is the present value or investment
I is the interest rate expressed as a fractional amount per compounding period-i.e., 5% is expressed as .05 n is the number of compounding periods.
(a) Create a MATLAB® function called future_value with three inputs: the investment (present value), the interest rate expressed as a fraction, and the number of compounding periods.
(b) Use your function to determine the value of a $1000 investment in 10 years, assuming the interest rate is 0.5% per month, and the interest is compounded monthly.
Problem 6.5 (page 235)
By rearranging the preceding relationship between moles and mass, you can find the mass if you know the number of moles of a compound:
m= n*MW
(a) Create a function M-file called mass that requires two vector inputs-the number of moles and the molecular weight-and returns the corresponding mass. Because you are providing vector input, it will be necessary to use the meshgrid function in your calculations.
(b) Test your function with the compounds listed in the previous problem, for values of n from 1 to 10.
Problem 6.8 (page 236)
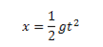
The distance a freely falling object travels is
where
g = acceleration due to gravity,
t = time in seconds
x = distance traveled in meters.
If you have taken calculus, you know that we can find the velocity of the object by taking the derivative of the preceding equation. That is,
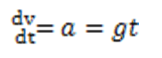
We can find the acceleration by taking the derivative again: