Reference no: EM132385402
COSC380/580 Algorithms in Machine Learning T2 2019
The University of New England
Assignment 3
Question 1
A single neuron is used as a binary classifier with the activation a = w0 + w1x1 + w2x2. Here w0 is the learned bias, w1 and w2 are the weights learned from the data and x1, x2 are the inputs. The output of the neuron is described by
y(a) = 1/(1 + e)-a
Using the initial weights w = (0, 1, 1) and η = 0.01 and the 3 inputs data below
|
x1
|
x2
|
target t
|
|
1
|
2
|
0
|
|
2
|
3
|
0
|
|
5
|
4
|
1
|
(a) Give the probabilities that the inputs belong to class 1.
(b) Provide the (hand) calculation for the first 2 iterations in the gradient-descent algorithm (i.e. provide the mathematical calculation in the "Activity rule" and the "Learning rule", updating wi then repeat the "Activity rule" and the "Learning rule" one more time). Write down the equations for the decision boundary in both iterations.
Show and justify all working.
Question 2
Apply a Bayesian approach to learning the parameters of the output function for a single neuron. This time, use Matlab to implement Hamiltonian Monte Carlo for the data set toy.dat. The target distribution will be the likelihood function for a single neuron, and gradient information is now required using this method. Name your file my single neuron.m. Give a contour plot of the learned function for the neuron output, as well as a plot of the sample autocorrelation. How much more efficent is this algorithm compared with Metropolis Monte Carlo?
Question 3
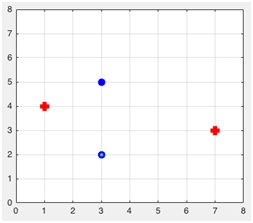
Given 4 data points in the figure above.
(a) Suggest a neural network model to correctly classify them. Justify your answer.
(b) Briefly describe how your model/algorithm works. Choose a set of initial values and show the calcula- tion for the first iteration.
Show and justify all working.