Reference no: EM13557
CASE 1
The diagram below shows a baffled tank with a six blade turbine agitator:
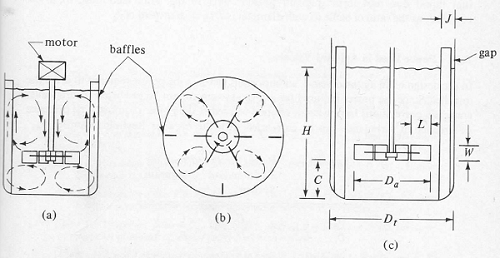
FIGURE 1
(a) Is a side view
(b) Is a bottom view
(c) Gives dimensions of the turbine and the tank.
It is important to note the dimensions given and identify them against the definitions you have been given. This tank contains baffles that are fitted to give a more favourable mixing profile. You should be able to identify the following:
Dt is the Tank Diameter
Da is the Turbine Diameter
C is the clearance of the Agitator from the bottom of the tank
W is the is the Turbine Width
L is a Turbine Internal Measurement
H is Liquid Height
J is Baffle Width
Without the baffles a swirling flow pattern develops. For vigorous agitation with vertical agitators baffles can be used to prevent swirling and improve the mixing. Usually 4 baffles are sufficient; their width is usually about 1/12 of the tank diameter. As in the first case study we considered in lectures, sometimes with large liquid depths 2 or 3 impellers are mounted on the same shaft; each acting as a separate mixer. The bottom impeller is usually 1 impeller diameter above the bottom of the tank.
If you use the type of agitator shown in the Figure 1 the geometric proportions are usually taken as:
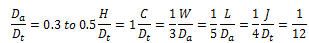
A typical curve for finding the Power Number for the type of impeller described is given below. This curve applies for Da/W = 5, and Dt/J = 12. The Reynolds Number can be calculated using the formula quoted on the 'Scale Up for Tanks' sheet.
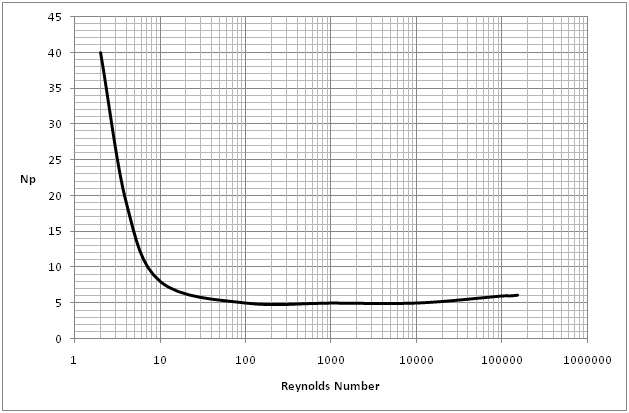
FIGURE 2
This type of tank is used in part of the production of a fine chemical such as aspirin. The first calculation we are required to do is to calculate a typical Power Consumption in the type of agitator and tank given in FIGURE 1. The Tank Diameter is Dt, the Turbine Diameter is Da, Dt = H and the Width is W. The individual values used for these parameters are given on a separate sheet (See below). The tank contains 4 baffles each having a width J. The Turbine is operated at N rpm and the liquid in the tank has a viscosity of mcp and density, r kg/m3.
i. Calculate the required power of the mixer in kW
ii. For the same conditions, except for the liquid having a value of m =100000 cp, calculate the required power and comment on your answer.
NOTE: Viscosity will normally have units of kg/ms which is Pa s.
1 cp is 1x10-3 Pa s. You would normally expect your initial calculated value of the power to be in J/s.
|
Dt(m)
|
Da(m)
|
W(m)
|
J(m)
|
N(rpm)
|
µ(cp)
|
P (kg/m3)
|
z
|
|
|
|
1.75
|
0.61
|
0.122
|
0.146
|
90
|
10
|
930
|
3.5
|
|
|
CASE 2
In the cases that we carried out in lectures we assumed that, in scaling up:
If the TIP Speed was constant then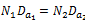 
(Note: Because Da and Dt are constructed at a fixed ratio we can also write, ) this
We also showed that when considering the Power/Unit Volume
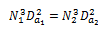and because Da and Dt are constructed at a fixed ratio we can also write,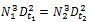 
This gives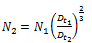 
Use the same agitation system as in CASE 1 and the previously given values of Dt, Da, W and J. This tank now needs to be scaled up to a vessel that has a volume Z times as large.This has to be done for the following requirements:
(a) Equal rates of mass transfer for the production of the fine chemical are required. This is often required for certain types of organic synthesis. Mass Transfer is usually occurring between solid-liquid phases or liquid-liquid phases
(b) Equal liquid motion is needed. This is often required for kinetically controlled systems where liquid blending is occurring.
When you have produced the scale up dimensions using geometric similarity, calculate the Power/Unit Volume for cases (a) and (b) and discuss the answers.
Studies show that for equal mass transfer in scale up that the 2/3 power equation should be used and for equal liquid motion the 1.0 power equation should be used.
CASE 3
In the Lectures where the necessary heat transfer area for the production of aspirin was being discussed, we had calculated (a) the volume of the scaled up version of the tank and the agitation rate (V = 1500 Litres and N = 630 rpm). We had also calculated (b) the heat transfer required from the steam jacket in the scaled up version to heat from 70oC to 80oC. (Heat Transferred = 76107.6 kJ/h). We now have to consider the necessary tank volume if the agitation intensity is unchanged , we are adding 200kg/h of crystals and we have heat transfer sufficient to keep the solution at 75oC.
The following guidance notes are given to extend the lecture notes:
The case study brief said that heating and dissolution of the crystals required 460 kJ/kg. Thus the energy needed is 460x200 = 92000kJ/h. This indicates that we need more heat transfer area then calculated in Part (b) of the study, thus we will have to increase the volume of the dissolution tank. If we ay that the new heat requirement is Q2:
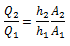
If we take the ratio of the heat transfer coefficients:
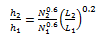................(1)
We had shown:
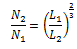
If this is substituted into equation (1)
This can be written as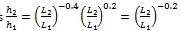 
Now we can write:
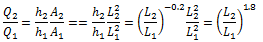
If we go back to our Pilot Plant where Q1 is 7290 kJ/h then we can calculate an adjusted volume.
