Write down the first few terms of each of the subsequent sequences.
1. {n+1 / n2}∞ n=1
2. {(-1)n+1 / 2n}∞ n=0
3. {bn} ∞ n=1, where bn = nth digit of ?
Solution
1. {n+1 / n2}∞ n=1
To obtain the first few sequence terms here all we require to do is plug in values of n into the formula given and we'll obtain the sequence terms.
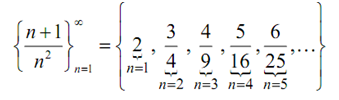
Note: Inclusion of the "..." at the end! This is a significant piece of notation as it is the just only thing that tells us that the sequence carries on and doesn't end at the last term.
(2) {(-1)n+1 / 2n}∞ n=0
This one is identical to the first one. The main variation is that this sequence doesn't initiate at n = 1.
{(-1) n+1 / 2n}∞ n=0 = {=1, ½ , - ¼ , 1/8, - 1/16, ....}
Note: The terms used in this sequence alternate in signs. Sequences of this type are sometimes known as alternating sequences.
(3) {bn} ∞ n=1, where bn = nth digit of ?
This sequence is not same from the first two in the sense that it doesn't have a particular formula for each term. Though, it does tell us what every term should be. Every term should be the nth digit of ?. So we know that ? = 3.14159265359....
After that the sequence is,
{3,1, 4,1, 5, 9, 2, 6, 5, 3, 5,...}