Steps for clip a line segment-PQ

• Initially, find all the points of intersections of the line segment PQ along with the edges of the polygonal window and describe them either as P_E and P_L points. Also find out the value of parameter t, by using equation (2) for respective PE's and PL's.

                                                            Or

If value of the normal to particular edges is not specified then, determine the value of normal to every edge of the window, then find out the value of parameter t, by using equation (2) for particular point of intersection among line segment and window edge then on the basis of the value of parameter t mark them like P_E and P_L given the value of t lies from 0 to 1 in magnitude.

• Secondly, out of the diverse values of t for P_E's find out the maximum value of t say it is t_max. Likewise, out of the diverse values of t for P_L's find out the minimum value of t say it be t_min . Remember here that for clipping to be possible t_min > t_max.
• at last, vary the parameter t from t_max to t_min and find out the clipped line as outcome.

For well understanding of steps here figure is shown below:

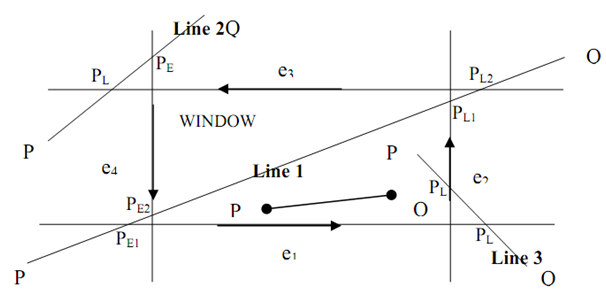
Figure: Steps of Cyrus Beck Clipping

During in case of Line 1: (PQ)

1) Point 1 is potentially entering (P_E1) since as we move along PQ, the LHS of e₁ is window and hence, it seems that we are entering the window.

2) Point 2 is again P_E2 same as point 1.

3) Point 3 is potentially leaving (P₄) ? as we move along PQ, the LHS of e₂ is window and hence, it seems that we are leaving the window.

4) As the same, point 4 is also P_L2.

Line 2 and 3 (PQ):

By using similar logic as for line 1 we determine p‾_L and PE. Here, it is to be noted that for all points of intersection we have several value of t.

Say t₁ is value of t for P_E1

Say t₂ is value of t for P_E2

Say t₃ is value of t for P_L1

Say t₄ is value of t for P_L2