This assignment will simulate large deformations (nonlinear geometry) and occurrence of necking and buckling due to static tensile and compressive loading of a given elastic-plastic ductile metallic material.

The aim of this assignment is the investigation of computationally effective solution methods to simulate unstable large deformations.

Assume the material to be aluminium. The characteristic curve in the plastic range can be fitted to a material law given by

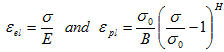, where E= 70GPa, s₀=200 MPa, B=3.0 GPa and H=4.0

Assume Poisson's ratio to be n=0.25.

1) Simulate the tension test for the following specimen geometry:

• The specimen has a 0.1*# mm width and thickness (solid square) cross-section with 0.4*# mm length

2) Simulate the compression test for the following specimen geometry:

• The specimen is a slender plate, 0.6*# mm height, 0.2*# mm width and 0.02*# mm thickness
• Include different imperfections (maximum out-of-plane centre imperfection is 50%, 100% and 200% of thickness) into your model for the nonlinear analysis.

For both models, # = 100 + the last two digits of your student number (e.g. for s123456 -> # = 156).

Introduce the given material properties into your models as discussed in lecture 3 on plasticity (you might want to use software such as Excel to generate the data). Apply appropriate boundary conditions for each loading case. Analyse results to reproduce the characteristic curve of the material as usual in analysing the results of experimental tests. This means that you need to produce force-displacement diagrams for each test (in-plane and out-of-plane when appropriate). Using constraints for the applied boundary conditions on the top plate are very useful in this case!

Simulate elongating both specimens statically by 25%.

Assume all models to be welded to rigid blocks at both ends. Due to these boundary conditions (fixed-fixed), determine why imperfections are required to introduce buckling in the nonlinear model, but necking occurs without imperfection. Determine the differences in the buckling response with different levels of imperfection.