Sample Mean Chart - Control Charts for Variables

This figure depicts a typical means chart, on which sample means would be progressively plotted, left to right. Two sets of control limits have been drawn symmetrically about the process population mean (estimated as the grand mean of several samples). The inner pair, the upper and lower warning limits, are positioned ±1.96 standard errors (s) above and below the population mean. For a stable process, there is a 1 in 40 chance that a sample mean will exceed the upper warning limit, and likewise for the lower warning limit. The outer pair, the upper and lower action limits, are positioned ±3.09s above and below the population mean. Again, for a stable process, there is only a 1 in 1000 chance of a sample mean breaching the upper limit, and likewise for the lower limit. If we determine the ranges of several samples, we can compute the average sample range (¯R). Remembering that the standard error s = σ / √n, we can take advantage of the findings of a statistician, Hartley, who quantified the relationship: σ = ¯R/d_n where d_n is a coefficient which varies with sample size. Hartley's constants (d_n), for sample sizes 2 to 6, are presented in this table.

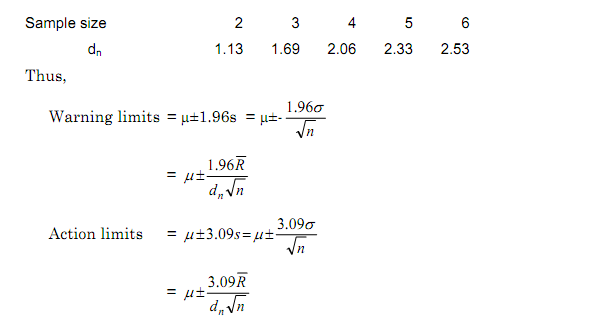
For convenience, the coefficients 1.96/d_n √n and 3.09/d_n √n have been calculated for a series of sample sizes. These values are presented as A' _0.025 and A' _0.001 in this table.

Sample size             A'0.025                A'0.001 

2                                  1.23                 1.94 

3                                  0.67                 1.05 

4                                  0.48                 0.75 

5                                  0.38                 0.59 

6                                   0.32                0.50

The final expressions are, therefore:

Warning limits = μ+A'_0.025 ¯R

Action limits = μ+A'_0.001 ¯R