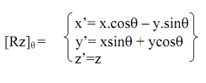Rotation about z-axis - Transformation for 3-d rotation

Rotation about z-axis is explained by the xy-plane. Suppose a 3-D point P(x,y,z) be rotated to P'(x',y',z') along with angle of rotation q see Figure 9. Because both P and P' lies upon xy-plane so z=0 plane their z components keeps similar as z=z'=0.

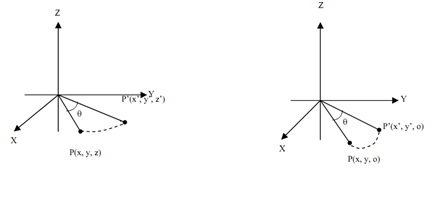
Figure a                                                                            Figure b

Thus, P'(x'y',0) be the effect of rotation of point P(x,y,0) making a +ive or anticlockwise angle φ with value of z=0 plane, as demonstration in Figure 10. From figure (10),

P(x,y,0) = P(r.cos φ,r.sin θ,0)

P'(x',y',0)=P[r.cos(φ + θ),rsin(φ + θ),0]

The coordinates of P' are as:

x'=r.cos(θ + φ) = r(cos θ cos φ - sin θ sin φ)

=x.cos θ - y.sin θ      (where x=rcos φ and y=rsin φ)

As the same;

y'= rsin(θ + φ)=r(sin θ cos φ + cos θ.sin φ)

=xsin θ +ycos θ

Hence,