Representation of Simplex method

We shall use the example previously stated for the graphical solution. The standard form of the model is given by:

Maximize :  Z = 3X_E + 2X₁ + OS₁ + OS₂ + OS₃ + OS₄
Subject to:  X_E + 2X_I + S₁ = 6

2X_E + X_I + S₂ = 8
-X_E + X_I + S₃ = 1
X_I + S₄ = 2

X_E, X_I, S₁, S₂, S₃, S₄ ≥ 0

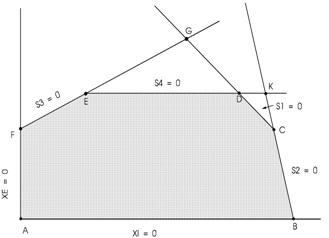
The figure depicts the solution space. Every point in this space can be represented in terms of the variables X_E, X_I, S₁, S₂, S₃ and S₄ of the standard form. (To show this point, observe that Si = 0, i = 1,2,3 and 4 turns the related equation into an edge of the solution space. For example: Si = 0 is equivalent to XE + 2XI = 6, which represents edge CD. Having S₁ > 0 will move the feasible points from edges toward the interior of the solution space).

Our main interest is to identify the extreme points algebraically. When we examine the figure we note that the values of X_E, X₁, S₁, S₂, S₃ and S₄ associated with the extreme points A, B, C, D, E, and F have the following definite pattern with regard to whether or not their values are equal to zero.

        Extreme           Zero                Non-zero
        Point             Variables            Variables

        A                    XE, XI               S1, S2, S3, S4
        B                    S2, XI               S1, XE, S3, S4
        C                    S2, SI               X1, XE, S3, S4
        D                    S4, SI               X1, XE, S3, S2
        E                    S4, S3               X1, XE, S1, S2
        F                    S4, XE               X1, S3, S1, S2

Two observations are instantly obvious:

Since the standard form has four equations and six unknowns, each extreme point must have two
 (= 6 - 4) variables at zero level.