Proof of Root Test 

Firstly note that we can suppose without loss of generality that the series will initiate at n = 1 as we've done for all our series test proofs.  As well note that this proof is very identical to the proof of the Ratio Test. Let us start off the proof here by suppose that 1 L < and we will need to illustrate that ∑a_n is absolutely convergent.  To do this let's first note that as L < 1 there is some number r like L < r < 1.

Now, remind that,

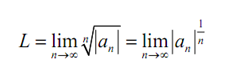
and because we as well as have chosen r such that  L< r there is some N like if  n ≥ N we will have,

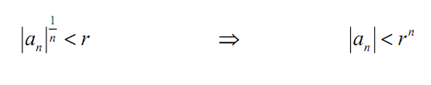
Here now the series

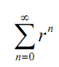
is a geometric series and as 0 < r < 1 we in fact know that it is a convergent series. As well because |a_n < rⁿ| n≥N  through the Comparison test the series

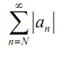
is convergent. Though since,

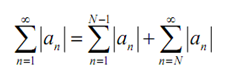
we are be familiar with that

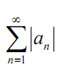
is as well convergent as the first term on the right is a finite sum of finite terms and hence finite.  Hence

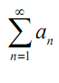
is absolutely convergent.

Subsequently, we need to assume that L >1 and we'll need to illustrate that ∑a_n is divergent. reminding that,

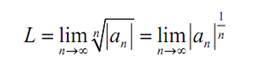
and as L > 1 we know that there should be some N such that if  n > N we will have,

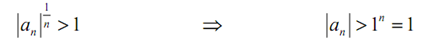
Though, if  |a_n| > 1 for all  n ≥ N after that we know that,

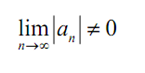
The meaning of this is like this:

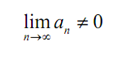
Hence, by the Divergence Test ∑a_n is divergent.

At last, we need to assume that L= 1and show that we could get a series which has any of the three possibilities.  To do this we just require a series for each case.  We'll leave the facts of checking to you but all three of the following series have L= 1 and each one shows one of the probabilities.