Solve x2 -10 < 3x .
Solution
There is a quite simple procedure to solving these. If you can memorize it you'll always be able to solve these kinds of inequalities.
Step 1: Get zero onto one side of the inequality. This doesn't matter which side contain the zero, though, we're going to be factoring into the next step thus keep that in mind as you do this step. Ensure that you've got something that's going to be easy to factor.
x2 - 3x -10 <0
Step 2 : If probable, factor the polynomial. Notice that it won't always be probable to factor this, however, that won't vary things. This step is actually here to simplify the procedure more than anything. Approximately all of the problems that we're going to look at will be factorable.
( x - 5) (x + 2) = 0
Step 3: Resolve where the polynomial is zero. Notice that this instance won't make the inequality true (in this case) since 0 < 0 is not a true inequality. That isn't a problem. These instances are going to let us to determine the actual solution.
The polynomial is zero at x = -2 & x = 5 .
Now, before moving on to the following step let's address why we desire these points.
We haven't discussed graphing polynomials still; though, the graphs of polynomials are pleasant smooth functions which have no breaks in them. It means that as we are moving across the number line (in any direction) if the value of the polynomial varies sign (say from positive to negative) then it ought to go through zero.
Thus, it means that these two numbers ( x = 5 and x = -2 ) are the only places where the polynomial can vary sign. Then the number line is divided into three regions. In each of region if the inequality is satisfied trhough one point from that region then this is satisfied for every point in that region. If it wasn't true (that means it was +ve at one point in the region and -ve at another) then it has to also be zero somewhere in that region, however that can't happen as already we've determined all the places where the polynomial can be zero! Similarly, if the inequality isn't satisfied for some of the instance in that region that it isn't satisfied for ANY point in that region. It leads us into the next step.
Step 4: Graph the instance where the polynomial value is zero (that means. the points from the earlier step) on a number line & pick a test point from each of the regions. Plug each test points into the polynomial and find out the sign of the polynomial at that point.
This is the step in the procedure that has all the work, though it isn't too bad. Here is the number line for this problem.
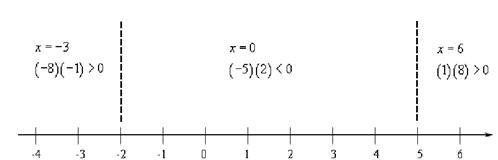
While we pick test points ensure that you pick easy numbers to work with. Thus, don't decide large numbers or fractions unless you are required to by the problem.
Also, note down that we plugged the test points into the factored from of the polynomial & all we're actually after here is whether or not the polynomial is +ve or -ve. Then, actually we didn't bother along with values of the polynomial just the sign & we can get that from the product illustrated. The product of two negatives value is a positive, etc.
We are now ready for the last step in the procedure.
Step 5 : Write down the answer. Remind that we discussed previous that if any point from a region satisfied inequality then all points within that region satisfied the inequality & similarly if any point from a region did not satisfy the inequality then none of the points within that region would satisfy the inequality.
It means that all we have to do is look up at the number line above. If the test point through a region satisfies the inequality then this region is part of the solution. If the test point doesn't satisfy the inequality then this region isn't .
Now, also take in that any value of x which will satisfy the original inequality will also satisfy the inequality from Step 2 and similarly, if an x satisfies the inequality from Step 2 then it will satisfy the original inequality.
Thus, that means that all we have to do is find out the regions wherein the polynomial from Step 2 is negative. For this problem i.e. only the middle region. The inequality & interval notation for the solution to this inequality are,
-2 < x < 5 ( -2, 5)
Notice that we do have to exclude the endpoints as we have a strict inequality (< in this case) in the inequality.
That appear like a long process, however, it actually isn't. There was much explanation in the earlier example. The remaining examples won't be as long since we won't need quite as much explanation in them.