Polygon Meshes - Modeling and Rendering

A polygonal surface to be sketched may not be easy and may have enormous curls and curves. Illustration: a crushed piece of paper or crushed piece of aluminum foil and so on. In these cases all sections of a polygonal surface can be produced as in computer graphics or can be simply drawn are with the assist of diverse standard graphic objects as rectangles, triangles, circles or may be semicircles, spheres or may be hemispheres and so on, drawn in a way that their pattern combination matches along with the polygonal surface about construction. Such cumulative combination of each standard graphic object is actually the mesh or polygonal mesh utilized to approximate the definite geometry of any complicated object about construction, with the assist of the standard graphic objects.

After studying the section of polygon tables, we understood that a polygonal surface can be represented along with the set of surfaces, set of edges and set of vertices; that are the common terminologies of nothing but graphs. Consequently we will use such concept here too, since the polygons we require to represent can be arbitrarily large. Hence, generally it is convenient and proper to utilize a polygon mesh quite than a single mammoth polygon as: single standard graphic object. For illustration, you can simplify the method of rendering polygons through breaking all polygons in triangles. Triangle renderers can also be executed in hardware, making it advantageous to break the world down in triangles. Observe the figure 8:

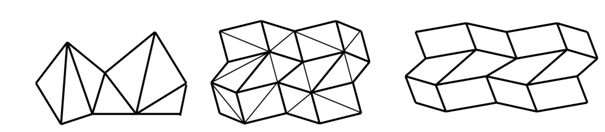
Figure  (a)                                   Figure  (b)                                           Figure  (c)

Another illustration where smaller polygons are good is the Inventor lighting model. Inventor calculates lighting at vertices and interpolates the values in the polygon's interiors. Through breaking larger surfaces in meshes of smaller polygons, the lighting approximation is enhanced. From the demonstrated Figure 8 two significant observations are:

-        Triangle mesh generates n-2 triangles from a polygon of n vertices.

-        Quadrilateral mesh generates (n-1) through (m-1) quadrilaterals from an n x m array of vertices

It is significant to note here specifying polygons, along with more than three vertices could consequence in sets of points, that are not co-planar, the purpose behind may be the numerical errors or error in choosing the coordinate position of the vertices. Handling non-coplanar vertices is quite complicated, thus two manners to handle theses situation:

• Break the polygon in triangles and also deal.
• Approximate A, B, and C in the plane equation, such can be done either with averaging or with projecting the polygon on the coordinate planes. A must be proportional to the projection as in the yz-plane, B proportional to xz as well as C proportional to xy. Better quality graphics system usually model objects along with polygon meshes and put system of a database of geometric and attribute information to assist processing of the polygon facets. Speedy hardware implemented polygon renderers are included in such systems along with the ability for displaying hundreds of thousands to one million or further shaded polygon per second consisting the application of surface texture.