Maximum shear stress - state of stress:

Consider the state of stress.

(a) According to principal stress theory the equivalent stress for this case is simply σ₁, i.e. 300 MPa.

(b) Let us consider principal strain theory.

The principal strain introduced in this case is as follows:

ε1 = 300/E -(0.3 × 200/E) = 240/E

This much of strain can be produced in uniaxial tension by a stress of 240 MPa and therefore, the equivalent stress according to principal strain theory is 240 MPa.

(c)        Maximum shear stress τ_max  =300 - 200/2 = 50 MPa .

This could be produced through a uniaxial stress of 100 MPa and thus equivalent stress according to shear stress theory is just 100 MPa.

(d)        Strain energy density, u = 1/2E [300² +200² -2×0.3×300×200]

=47000/E                                                                                 . . .(i)

If the equivalent uniaxial stress is σ_e, then u = σ²e/2E          . . .       (ii)

i.e. σ²e/2E  =47000/E

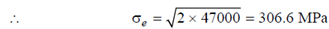
Distortion energy density

u_d  = 1/12G[(300-200)² +300²+200²] = 70000/6G

If equivalent uniaxial stress is σ, then

u_d  = 1/12G(σ²_e +σ²_e) = σ²e/6G  

i.e. σ²e/6G    =70000/6G

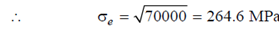
Even by we have previously analysed whether the solid is safe or not according to various theories, only through evaluating the equivalent stress, we are able to get an idea of the margin of safety according to every of the theories.