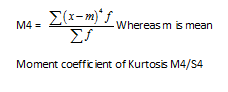Leptokurtic
a) A frequency distribution which is lepkurtic has normally a higher peak than that of the general distribution. The coefficient of kurtosis while determined will be found to be more than 3. Hence frequency distributions along with a value of more than three are definitely leptokurtic
b) Several frequency distributions while plotted may produce a curve similar to that of the general distribution. That frequency distributions are referred to as mesokurtic. The degree of kurtosis is normally equal to 3
c) While the frequency curve contacted produces a peak which is lower than that of a common distribution while such a curve is said to be platykurtic. The coefficient of Leptokurtic is generally less than 3
- This is necessary to calculate the numerical measure of kurtosis. The generally used measure of kurtosis is the percentile coefficient of kurtosis. This coefficient is commonly determined by using the given equation
Percentile measure of kurtosis, K (Kappa) =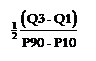
Illustration
Refer to the table above for loans to small business firms/units
Essential
Calculate the percentile coefficient of Kurtosis as
P90 = (90/100)(n + 1) = 0.9 (610 + 1)
= 0.9 (611)
= 549.9
The actual loan for a firm in this position
(549.9) = 80.5 + ((549.9 - 538)/40) x 5 = 81.99
P10 = (10/100) (n + 1) = 0.1 (611) = 61.1
The actual loan value given to the firm on this position is
50.5 +((61.1 - 32)/62) x 5 = 52.85
= 0.9 (611)
= 549.9
∴ percentile measure of kurtosis
K(Kappa) = ½ {(Q3 - Q1)/(P90 - p10)}
= ½ {(73.82 - 58.53)/(81.99 - 52.85)}
= 0.26
Because 0.26 < 3, it can be concluded that the frequency distribution exhibited by the distribution of loans is platykurtic
Kurtosis is measured also by moment statistics that utilize the exact value of each observation.
i. M1 the first moment = M1 = (åX)/n = Mean M1 or M1
M2 = (åX2)/n
M3 = (åX3)/n
M4 = (åX4)/n
3. M2 second moment about the mean M2 or f2
M2 = M2 - M12
4. M3 third moment about the mean M3 (a measure of the absolute skew ness)
M3 = M3 - 3M2M1 + 2M13
5. M4 fourth moment about the mean M4 (a measure of the absolute Kurtosis)
M4 = M4- 4M3M1 + 6M2M12 + 3M14
An alternative formula