Internal and external diameters - solid shaft:

Two shafts are of the similar material, length & weight. One is solid & of 100 mm diameter, the outer is hollow. If hollow shaft is to be store 25% more energy than the solid shaft while transmitting torque, what should be its internal & external diameters? Consider the similar maximum shear stress in both the shafts.

Solution

Consider A is the solid shaft of diameter D_a & B is the hollow shaft with external diameter D_b & internal diameter d_b. As both of the shafts are to be the similar material and of equal weight, their volumes must be equal.

Therefore,

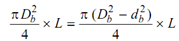
or

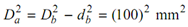
As the maximum shear stress is the similar for both the shafts, we have,

                                 τ_a  = τ_b

                           T_a D_a  /2J a = T_b D_b/2J B   ( since τ = T × r/ J = T × D/2J )

Therefore,

Ta/ Tb  = D_b/ D_a  × J _a/ J_b

But it is also given that the strain energy of B = 1.25 × strain energy of A.

Thus,

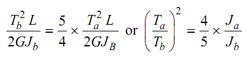
From the relationship, this reduces to

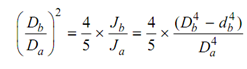
After that,  ∴

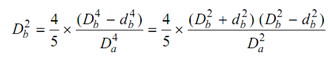
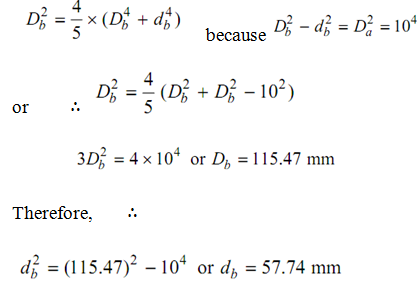
Therefore, the internal & external diameters of the hollow tube are 57.74 mm & 115.47 mm, respectively.