Index Shift - Sequences and Series

The main idea behind index shifts is to start a series at a dissimilar value for whatever the reason (and yes, there are legitimate reasons for doing that).

Consider the following series,

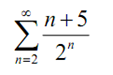
Assume that for some reason we wanted to start this series at n = 0 , but we did not wish to change the value of the series. The meaning of this is that we can't just change the n = 2 to n = 0 as this would add in two new terms to the series and so change its value.

Carrying out an index shift is a quite simple process to do. We'll start by describing a new index, say i, as follows,

i = n - 2

Here now, when n = 2, we will get i = 0 . Notice as well that if n = ∞ then i = ∞- 2 = ∞ , so only the lower limit will alter here. Next, we can solve this for n to get,

n = i + 2

We can now totally rewrite the series in terms of the index i in place of the index n just by plugging in our equation for n in terms of i.

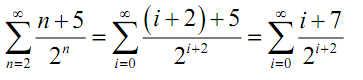
To end the problem out we'll remind that the letter we employed for the index doesn't matter and thus we'll change the final i back into an n to get,

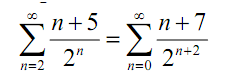
To induce you that these really are similar summation let us write out the first couple of terms for each one of them,

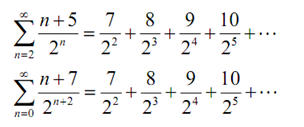
Thus, sure enough the two series do have exactly similar terms.

In fact there is an easier way to do an index shift. The method described above is the technically right way of doing an index shift. Though, notice in the above instance we decreased the initial value of the index by 2 and all the n's in the series terms increased by 2 also. This will all time work in this way.  If we decrease the initial value of the index by a set amount as compared to all the other n's in the series term will increase by similar amount. Similarly, if we increase the initial value of the index by a set amount, after that all the n's in the series term will decrease by similar amount.