Indeterminate forms

Limits we specified methods for dealing with the following limits.

In the first limit if we plugged in x = 4 we would get 0/0 & in the second limit if we "plugged" within infinity we would get ∞ /-∞ (recall that as x goes to infinity polynomial will act in the similar fashion that its largest power behaves). Both are called indeterminate forms.  In both cases there are competing interests or rules & it's not clear which will win out.

In the case of 0/0 typically we think of a fraction which has a numerator of zero as being zero. Though, we also tend to think of fractions wherein the denominator will zero as infinity or may not exist at all.  Similarly, we tend to think of a fraction wherein the numerator & denominator are the similar as one.  Therefore, which will win out?  Or will neither win out and they all will "cancel out" and the limit will attain some other value?

In the case of ∞ /-∞ we contain a similar set of problems.  If the numerator of fraction will be infinity we tend to think of the whole fraction will be infinity.  Also if the denominator will be infinity we tend to think of the fraction will be zero. We also have the case of a fraction wherein the numerator & denominator are the similar (ignoring the minus sign) and thus we might get -1.  Again, it's not apparent which of these will win out, if any will win out.

Along the second limit there is the further problem which infinity isn't actually a number and therefore we actually shouldn't even treat it as a number.  Most of time it simply won't behave as we would expect it to if it was a number.

It is the problem with indeterminate forms.  It's just not apparent what is happening in the limit. There are other kinds of indeterminate forms as well. Some other kinds are following,

(0) ( ± ∞ )         1^∞       0⁰                 ∞⁰            ∞ - ∞

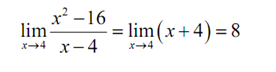
These all contain competing interests or rules which tell us what have to happen and it's just not apparent which, if any, of the interests or rules will win out.

For the two limits above we work on them as follows.

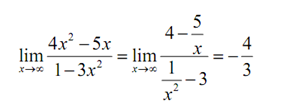
In the first case simply we factored, canceled & took the limit and in the second case we factored out an x² from both the numerator & the denominator and took the limit. Notice that none of the competing interests or rules in these instance won out! That is frequently the case.

Thus we can deal with some of these.  Though what about the following two limits.

First is a 0/0 indeterminate form, however we can't factor this one.  The second is an  ∞ /∞   indeterminate form, however we can't just factor an x² out of the numerator.