Description
A heap is an efficient tree-based data structure that can be used as a priority queue. Recall that the abstract data type of a priority queue has the following operations
- size, isEmpty, min
- insert
- removeMin
We can describe the priority queue ADT using the following Java Entry class and interface:
1 import java.lang.Comparable;
2
3 /**
4 * When items are added to the heap, you should create an Entry object
5 * to hold the key and value and store this in the appropriate node
6 */
7 public class Entryextends Comparable,V> {
8 protected K key;
9 protected V value;
10 public MyEntry(K k, V v) { key = k; value = v; }
11 public K getKey() { return key; }
12 public V getValue() { return value; }
13 public String toString() { return "(" + key + "," + value + ")"; }
14 }
15
16 public interface PriorityQueueextends Comparable,V> {
17 /** Returns the number of items in the priority queue. */
18 public int size();
19 /** Returns whether the priority queue is empty. */
20 public boolean isEmpty();
21 /** Returns but does not remove an entry with minimum key. */
22 public Entry min();
23 /** Inserts a key-value pair and return the entry created. */
24 public Entry insert(K key, V value);
25 /** Removes and returns an entry with minimum key. */
26 public Entry removeMin();
27 }
The main operations (insert, removeMin) can be done in O(log n) with a heap, while the other operations of the priority queue ADT (isEmpty, size, or look up the min value) are constant time. In lectures we have seen how to implement a heap using an array-based implementation.
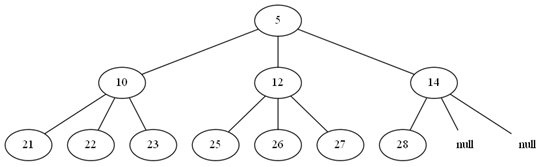
Figure 1: 3-way heap example
For this assignment you must implement a min-heap using a using a tree-based implementation (similar to the binary tree class we have used in tutorials). This tree should be 3-way tree, where each node needs to have (at most) three children
Note that the definition of a 3-way heap is identical to that of a binary heap, except for allowing at most three children (see Figure ). As with a binary tree, every node must have all of its children, except for the nodes at the last levels of the tree. In more detail, your task is to
1. Design a 3-way tree structure that you will use for building your heap. You can use code provided in the book. You can use any helper data structures that you need (linked lists, arrays etc.), but you must implement the tree structure yourself.
2. Implement your design for a generic 3-way heap in a class called ThreewayHeap. You will need to implement all operations (insert, removeMin, isEmpty, etc.) in the supplied interface and skeleton for the 3-way heap. In most cases the extension is straightforward from binary heaps, with certain extra cases that you need to check.
3. Include a method in your heap to print out a visual representation in DOT format (helpful for testing/debugging purposes).
4. Design test cases for your new heap structure, used as a priority queue
5. Use the provided test code on your implementation