How do you traverse a Binary Tree?  Describe Preorder, Inorder and Postorder traversals with example.    

Ans: Traversal of tree means tree searching for a aim. The aim may be for searching or sorting of the items consisted of in a tree. A tree may consist of an item at its node as a label.

Traversing a tree is a recursive process. 

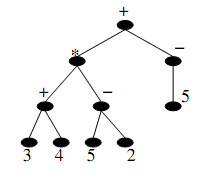
To apply this, a tree is considered to comprise three components: root, left subtree and right subtree. These three components can be in order in six different ways: (left, root, right), (root, left, right), (left, right, root), (right, left, root), (right, root, left) and (root, right, left). The first three are used while the last three combinations are of no make use of as it alters the positions of a node in a positional tree.

Inorder Traversal: In this type of traversal, a tree is traversed in the sequence: Left subtree, Root, Right subtree.   

In the above expression, start at the root node marked, +. As first we have to traverse its left subtree, thus move to the root of left subtree that is node marked, *. Once again it has a left subtree with root node marked +, visit it. This subtree has a node labeled 3 that has no left subtree, thus out put 3. Then root of this subtree that is '+' and then right subtree which is once again a node labeled with 4, so output it. So we have expression acquired till here is 3 + 4.

Proceeding this way we acquire (3+4)*(5-2) + (-5). Parentheses signify both precedence and portion of the sub tree to which this sub-expression corresponds.     

Preorder Traversal: In this type of traversal a tree is traversed in the sequence: Root, Left subtree, Right subtree. Apply the algorithm recursively till all nodes have been visited, we acquire + * + 3 4 - 5 2 -5. 

Postorder Traversal: In this type of traversal a tree is traversed in the sequence: Left subtree, Right subtree, Root. We acquire 3 4 + 5 2 - * 5 - +.