Health Insurance and Its Interaction with Medical Market
Health insurance is important to the demand and supply considerations of health care as well as in determining the government's role in allocating resources. Health insurance is a type of 'cost sharing' whereby the insurer pays the medical costs if the insured becomes sick due to causes covered. The insurer may be a private organization or a government agency. Market-based health care systems such as that in the United States rely on private medical insurance.
The concept of health insurance is more applicable in developed economies. In developed countries majority of the persons do not pay directly for their health care. Rather the insurance companies pay for much of the medical care with the consumer paying a small portion of the total health care expenditure. Insurance coverage is provided through the payment of the premiums (in privately financed systems) or taxes (when the insurance is provided publicly). The premiums are often, although not always, paid through the consumer's participation in the labour force.
The concept of health insurance involves the theory of expected utility with the underlying concepts of marginal benefit and cost. The consumers' demand for health insurance represents the amount of insurance coverage a person is willing to buy at suitable premiums. Additional insurance coverage will be purchased if the premium (price) declines. Thus, when the marginal benefit of the consumer to the additional coverage equals the cost of buying that insurance, then other things being equal, the optimal amount of insurance will be purchased. The demand for health insurance is related to the considerations underlying the purchase of insurance. It is assumed that an individual wishes to maximize his or her utility which is the usual assumption made in demand analysis. Since a person does not know how he will be affected by an illness requiring a loss of wealth to pay for it, the individual seeks to maximise his or her expected utility by choosing from the two alternatives:
(i) He can purchase insurance and thereby incur a small loss in the form of the insurance premium, or
(ii) He can self-insure, which means either facing the small possibility of a large loss in the event of illness, or the large possibility that the medical loss will not occur.
Given the above two choices, one can select one's choice by ranking the choices according to how much of one choice is preferred over the other. Though there is no unique point of origin for measuring the utility function, subject to a certain point of origin being accepted, the utility function of an individual can be described for varying levels of wealth. Such an utility function, following the rule of the diminishing marginal utility, can be graphically shown as in Figure-1. Now, to determine whether or not to purchase health insurance, let us assume that if an illness occurs it will cost Rs. 8000. Consider the individual to be currently at wealth level W3 signifying a income level of Rs.10000. If the illness occurs, Rs. 8000 will be paid out as a result of which his wealth will shrink to the level W1. The corresponding levels of utility for wealth levels W3 and W1 are U3 and U1 (upper panel in Figure 1). Note that in the lower panel, the graph incorporates the expected utility in addition to the total utility. Now, assuming that the probability of occurring illness is 0.025 (i.e. 2.5 percent) and the cost of the treatment is Rs. 8000, the premium to cover this risk would be 0.025 X Rs.8000 = Rs. 200.
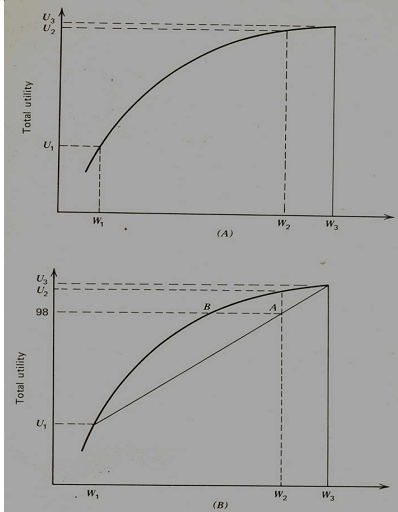
Utility Function at Varying Levels of Income
Given the above situation, if the person were to buy insurance at the actuarial value of the loss, then he would pay Rs. 200, whereupon his wealth reduces to the level of W2 (representing Rs. 9800) with a corresponding utility level of U2 . Thus, the choices facing the individual between purchasing the insurance and taking the risk of self-spending for the illness becomes:
(a) Purchase insurance for Rs. 200 and move to a marginally lower level of utility (i.e. U2) or;
(b) Not purchase insurance and face a 2.5 per cent chance that he will incur Rs. 8000 loss and thereby move to a much lower utility level of U1 associated with a reduced wealth position of Rs. 2000 or alternatively face a high probability of 97.5 per cent that a loss will not be incurred and thereby remain at a wealth position of Rs. 10000 with an associated utility level of U3 (say, equal to 100). In order to compare the relative positions of choices at 'a' and 'b', we can calculate the expected utility levels (which is the weighted sum of the utilities of outcomes with weights being the probabilities of each outcome). Thus, the expected utility of choice 'b' is: P(U1) + (1-P)(U3) = 0.025 (20) + 97.5 (100) = 98.
To determine whether a person should buy health insurance, we compare the utility of choice 'a' which represents purchasing insurance thereby leaving the person at utility level U2 . Since the utility level of choice 'a' is evidently greater than that of choice 'b', it is more advantageous to purchase the insurance. Note that in panel A of the diagram above, the curve represents the expected utility for different probabilities that the illness will occur. The lower the probability that the event will occur the closer the expected utility will be to the point farthest to the right on the utility curve. Thus, the factors of demand for health insurance can be identified as:
(i) How risk averse the individual is;
(ii) The probability of occurring the event of illness;
(iii) The magnitude of the loss associated with the event of illness for a person;
(iv) The price of insurance; and
(v) The income of the individual who will take the health insurance (i.e. question of affordability and capability of the cost of health care associated with the level of income).
The demand for health insurance is therefore affected by variables like:
(i) The cost or price of health care,
(ii) Income level of the individual,
(iii) Tastes towards risk aversion and thereby preference for buying insurance and
(iv) The size of the probable loss.