A striking application of DFS is determine a strongly connected component of a graph.

Definition: For graph G = (V, E) , where V refer to the set of vertices and E refer to the set of edges, we described a strongly connected components as follows:

U refers to a sub set of V such that u, v linked to U such that, there is a path from u to v and v to u. That is, all of the pairs of vertices are reachable from each other.

In this section we shall use another concept called transpose of any graph. Given a directed graph G a transpose of G is described as G^T. G^T is described as a graph along with the same number of vertices & edges with only the direction of the edges being reversed. G^T is attained by transposing the adjacency matrix of the directed graph G.

The algorithm for determining these strongly connected components uses the transpose of G, G^T.

G = ( V, E ), G^T = ( V, E^T ), where E^T = {  ( u, v ): ( v, u ) belongs to E }

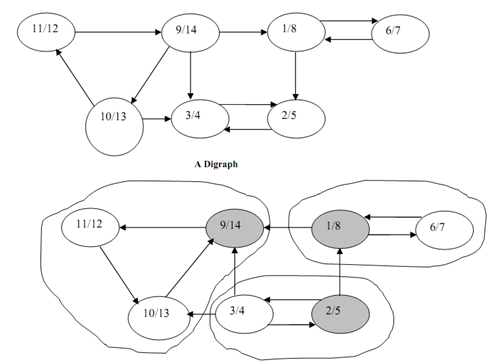
Figure: Transpose and strongly connected components of digraph of above Figure

Figure illustrates a directed graph along with sequence in DFS (first number of the vertex illustrates the discovery time and second number illustrates the finishing time of the vertex during DFS. Figure illustrates the transpose of the graph in Figure whose edges are reversed. The strongly connected components are illustrated in zig-zag circle in Figure.

To determine strongly connected component we begun with a vertex with the highest finishing time and begun DFS in the graph GT and then in decreasing order of finishing time. DFS along vertex with finishing time 14 as root determine a strongly connected component. Alike, vertices along finishing times 8 and then 5, while chosen as source vertices also lead to strongly connected components.