Find out the hydrostatic force on the following triangular plate that is submerged in water as displayed.

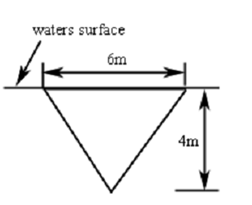
Solution

The first thing to do here is set up an axis system.  Thus, let's redo the diagram above with the following axis system added in.

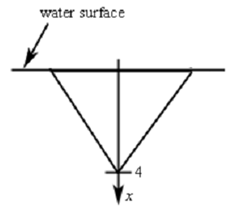
Thus, we are going to orient the x-axis that is why positive x is downward, x = 0 corresponds to the water surface and x = 4 refers to the depth of the tip of the triangle. After that we break up the triangle into n horizontal strips every equal width Δx and in each interval [x_i-1,x_i] select any point x_i* .

To make the computations easier we are going to make two assumptions about these strips. First, we will ignore the fact that in fact the ends are going to be slanted and presume the strips are rectangular. If Δx is adequately small this will not affect our computations much.

Second, we will assume that Δx is small enough that the hydrostatic pressure on every strip is necessarily constant. Below is a representative strip.

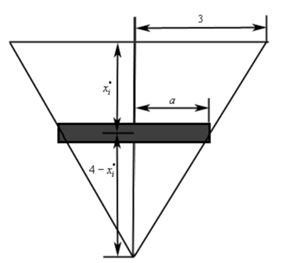
The height of this strip is Δx and the width is 2a.  We can use identical triangles to determine a as follows,

¾ = a / 4-x_i*

= a 3- ¾ x_i*

Here now, as we are assuming the pressure on this strip is constant, the pressure is illustrated by,

P_i = ρgd = 1000 (9.81) x_i*

= 9810 x_i*

and the hydrostatic force on every strip is,

F_i = P_i A = P_i (2aΔx)

= 9810 x_i* (2) (3- (3/4) x_i*)Δx

=19620 x_i* (3- (3/4) x_i*)Δx

The estimated hydrostatic force on the plate is then the sum of the forces on all the strips or,

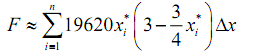
Taking the limit will obtain the exact hydrostatic force,

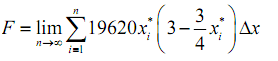
By using the definition of the definite integral this is nothing much more than,

F = ∫⁴₀ 19620 (3x - ¾ x²) dx

The hydrostatic force is then

F = ∫⁴₀ 19620 (3x - ¾ x²) dx

= 19620 (3/2 x² - ¼ x³) |⁴₀

= 156960 N